ayeimanolr

I am revising my previous posts on the whole process, from getting started with R to using it to do linear modelling and linear mixed-effects modelling.

Sunset over the coast, on the road from Ravenglass to Broughton

What this revision will entail is some rewriting of .R provided code, some updating, some extension. Extensions will focus on model comparison methods, information criteria approaches to model evaluation, and the choices one must make in data analysis.

 

 

 

For an example analysis, we collated a .csv file of data from a repeated measures lexical decision experiment, which can be downloaded here. The code I have used in running the analysis described in this post can be found here.

This file holds data on:

1. participant attributes;

2. word attributes;

3. participant responses to words in the lexical decision task.

In this post, I want to take a quick look at how you would actually run a mixed-effects model, using the lmer() function furnished by the lme4 package, written by Doug Bates (Bates, 2010 – appears to a preprint of his presumed new book, see also Pinheiro & Bates, 2000). A useful how-to guide, one I followed when I first started doing this kind of modelling, is in Baayen (2008). An excellent, and very highly cited, introduction to mixed-effects modelling for psycholinguistics, is found in Baayen, Davidson & Bates (2008).

First, then, we enter the following lines of code to load the libraries we are likely to need, to set the working directory to the folder where we have copied the full database, and to read that database as a dataframe in the session’s workspace:

Load libraries, define functions, load data

We start by loading the libraries of functions we are likely to need, defining a set of functions not in libraries, setting the working directory, and loading the dataframe we will work with into the R session workspace.

# load libraries of packages #############################################################################
library(languageR)
library(lme4)
library(ggplot2)
library(grid)
library(rms)
library(plyr)
library(reshape2)
library(psych)
library(gridExtra)

# define functions #######################################################################################
# pairs plot function

#code taken from part of a short guide to R
#Version of November 26, 2004
#William Revelle
# see: http://www.personality-project.org/r/r.graphics.html

panel.cor <- function(x, y, digits=2, prefix="", cex.cor)
{
usr <- par("usr"); on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r = (cor(x, y))
txt <- format(c(r, 0.123456789), digits=digits)[1]
txt <- paste(prefix, txt, sep="")
if(missing(cex.cor)) cex <- 0.8/strwidth(txt)
text(0.5, 0.5, txt, cex = cex * abs(r))
}
# just a correlation table, taken from here:
# http://myowelt.blogspot.com/2008/04/beautiful-correlation-tables-in-r.html
# actually adapted from prvious nabble thread:

corstarsl <- function(x){
require(Hmisc)
x <- as.matrix(x)
R <- rcorr(x)$r
p <- rcorr(x)$P

## define notions for significance levels; spacing is important.
mystars <- ifelse(p < .001, "***", ifelse(p < .01, "** ", ifelse(p < .05, "* ", " ")))

## trunctuate the matrix that holds the correlations to two decimal
R <- format(round(cbind(rep(-1.11, ncol(x)), R), 2))[,-1]

## build a new matrix that includes the correlations with their apropriate stars
Rnew <- matrix(paste(R, mystars, sep=""), ncol=ncol(x))
diag(Rnew) <- paste(diag(R), " ", sep="")
rownames(Rnew) <- colnames(x)
colnames(Rnew) <- paste(colnames(x), "", sep="")

## remove upper triangle
Rnew <- as.matrix(Rnew)
Rnew[upper.tri(Rnew, diag = TRUE)] <- ""
Rnew <- as.data.frame(Rnew)

## remove last column and return the matrix (which is now a data frame)
Rnew <- cbind(Rnew[1:length(Rnew)-1])
return(Rnew)
}

# read in data files #####################################################################################

getwd()
# set the working directory

setwd("[maybe file downloaded to Downloads folder--see getinfo in Finder")

# read in the full database

RTs.norms.subjects <- read.csv("RTs.norms.subjects 090513.csv", header=T, na.strings = "-999")

If you run all that code, you will see the dataframes and functions appear listed in the workspace window of R-studio.

Prepare data – remove errors

As in the previous post, we need to remove errors from the dataframe. We can do this by setting a condition on rows, subsetting the dataframe to a new dataframe where no RT is less than zero because DMDX outputs .azk datafiles in which incorrect RTs are listed as negative numbers.

# preparing our dataframe for modelling ##################################################################
# the summary shows us that there are negative RTs, which we can remove by subsetting the dataframe
# by setting a condition on rows

nomissing.full <- RTs.norms.subjects[RTs.norms.subjects$RT > 0,]

# inspect the results

summary(nomissing.full)

# how many errors were logged?

# the number of observations in the full database i.e. errors and correct responses is:

length(RTs.norms.subjects$RT)

# > length(RTs.norms.subjects$RT)
# [1] 5440

# the number of observations in the no-errors database is:

length(nomissing.full$RT)

# so the number of errors is:

length(RTs.norms.subjects$RT) - length(nomissing.full$RT)

# > length(RTs.norms.subjects$RT) - length(nomissing.full$RT)
# [1] 183

# is this enough to conduct an analysis of response accuracy? we can have a look but first we will need to create
# an accuracy coding variable i.e. where error = 0 and correct = 1

RTs.norms.subjects$accuracy <- as.integer(ifelse(RTs.norms.subjects$RT > 0, "1", "0"))

# we can create the accuracy variable, and run the glmm but, as we will see, we will get an error message, false
# convergence likely due to the low number of errors

Notice:

— I am copying the outputs from function calls from the console window, where they appear, into the script file, where they are now saved for later reference.

— I find this to be a handy way to keep track of results, as I move through a series of analyses. This is because I often do analyses a number of times, maybe having made changes in the composition of the dataframe or in how I transformed variables, and I need to keep track of what happens after each stage or each operation.

— You can see that there were a very small number of errors recorded in the experiment, less than 200 errors out of 5000+ trials. This is a not unusual error rate, I think, for a dataset collected with typically developing adult readers.

In this post, I will add something new, using the ifelse() control structure to create an accuracy variable which is added to the dataframe:

# so the number of errors is:

length(RTs.norms.subjects$RT) - length(nomissing.full$RT)

# > length(RTs.norms.subjects$RT) - length(nomissing.full$RT)
# [1] 183

# is this enough to conduct an analysis of response accuracy? we can have a look but first we will need to create
# an accuracy coding variable i.e. where error = 0 and correct = 1

RTs.norms.subjects$accuracy <- as.integer(ifelse(RTs.norms.subjects$RT > 0, "1", "0"))

# we can create the accuracy variable, and run the glmm but, as we will see, we will get an error message, false
# convergence likely due to the low number of errors

Notice:

— I am starting to use the script file not just to hold lines of code to perform the analysis, not just to hold the results of analyses that I might redo, but also to comment on what I am seeing as I work.

— The ifelse() function is pretty handy, and I have started using it more and more.

— Here, I can break down what is happening step by step:-

1. RTs.norms.subjects$accuracy <- — creates a vector that gets added to the existing dataframe columns, that vector has elements corresponding to the results of a test on each observation in the RT column, a test applied using the ifelse() function, a test that results in a new vector with elements in the correct order for each observation.

2. as.integer() — wraps the ifelse() function in a function call that renders the output of ifelse() as a numeric integer vector; you will remember from a previous post how one can use is.[datatype]() and as.[datatype]() function calls to test or coerce, respectively, the datatype of a vector.

3. ifelse(RTs.norms.subjects$RT > 0, “1”, “0”) — uses the ifelse() function to perform a test on the RT vector such that if it is true that the RT value is greater than 0 then a 1 is returned, if it is not then a 0 is returned, these 1s and 0s encode accuracy and fill up the new vector being created, one element at a time, in an order corresponding to the order in which the RTs are listed.

I used to write notes on my analyses on paper, then in a word document (using CTRL-F that will be more searchable), to ensure I had a record of what I did.

It is worth keeping good notes on what you do because you (I) rarely get an unbroken interval of time in which to complete an analysis up to the report stage, thus you will often return to an analysis after a break of days to months, and you will therefore need to write notes that your future self will read so that analyses are self-explanatory or self-explained.

Check predictor collinearity

The next thing we want to do is to examine the extent to which our predictors cluster, representing overlapping information, and presenting potential problems for our analysis. We can do this stage of our analysis by examining scatterplot matrices and calculating the condition number for our predictors. Note that I am going to be fairly lax here, by deciding in advance that I will use some predictors but not others in the analysis to come. (If I were being strict, I would have to find and explain theory-led and data-led reasons for including the predictors that I do include.)

# check collinearity and check data distributions #########################################################
# we can consider the way in which potential predictor variables cluster together

summary(nomissing.full)

# create a subset of the dataframe holding just the potential numeric predictors
# NB I am not bothering, here, to include all variables, e.g. multiple measures of the same dimension

nomissing.full.pairs <- subset(nomissing.full, select = c(

 "Length", "OLD", "BG_Mean", "LgSUBTLCD", "brookesIMG", "AoA_Kup_lem", "Age",
 "TOWRE_wordacc", "TOWRE_nonwordacc", "ART_HRminusFR"

 ))

# rename those variables that need it for improved legibility

nomissing.full.pairs <- rename(nomissing.full.pairs, c(

 brookesIMG = "IMG", AoA_Kup_lem = "AOA",

 TOWRE_wordacc = "TOWREW", TOWRE_nonwordacc = "TOWRENW", ART_HRminusFR = "ART"

 ))

# subset the predictors again by items and person level attributes to make the plotting more sensible

nomissing.full.pairs.items <- subset(nomissing.full.pairs, select = c(

 "Length", "OLD", "BG_Mean", "LgSUBTLCD", "IMG", "AOA"

))

nomissing.full.pairs.subjects <- subset(nomissing.full.pairs, select = c(

"Age", "TOWREW", "TOWRENW", "ART"

))

# draw a pairs scatterplot matrix

pdf("ML-nomissing-full-pairs-items-splom-110513.pdf", width = 8, height = 8)

pairs(nomissing.full.pairs.items, lower.panel=panel.smooth, upper.panel=panel.cor)

dev.off()

# draw a pairs scatterplot matrix

pdf("ML-nomissing-full-pairs-subjects-splom-110513.pdf", width = 8, height = 8)

pairs(nomissing.full.pairs.subjects, lower.panel=panel.smooth, upper.panel=panel.cor)

dev.off()

# assess collinearity using the condition number, kappa, metric

collin.fnc(nomissing.full.pairs.items)$cnumber
collin.fnc(nomissing.full.pairs.subjects)$cnumber

# > collin.fnc(nomissing.full.pairs.items)$cnumber
# [1] 46.0404
# > collin.fnc(nomissing.full.pairs.subjects)$cnumber
# [1] 36.69636

You will see when you run this code that the set of subject attribute predictors (see below) …

… and the set of item attribute predictors (see below) …

… include some quite strongly overlapping variables, distinguished by high correlation coefficients.

I was advised, when I started doing regression analyses, that a rule-of-thumb one can happily use when examining bivariate i.e. pairwise correlations between predictor variables is that there is no multicollinearity to worry about if there are no coefficients greater than however, I can think of no statistical reason for this number, while Baayen (2008) recommends using the condition number, kappa, as a diagnostic measure, based on Belsley et al.’s (1980) arguments that pairwise correlations do not reveal the real, underlying, structure of latent factors (i.e. principal components of which collinear variables are transformations or expressions).

If we calculate the condition number for, separately, the subject predictors and the item predictors, we get values of 30+ in each case. Baayen (2008) comments that (if memory serves) a condition number higher than 12 indicates a dangerous level of multicollinearity. However, Cohen et al. (2003) comment that while 12 or so might be a risky kappa there are no strong statistical reasons for setting the thresholds for a ‘good’ or a ‘bad’ condition number; one cannot apply the test thoughtlessly. That said, 30+ does not look good.

The condition number is based around Principal Components Analysis (PCA) and I think it is worth considering the outcome of such an analysis over predictor variables when examining the multicollinearity of those variables. PCA will often show that  set of several item attribute predictors will often relate quite strongly to a set of maybe four orthogonal components: something to do with frequency/experience; something relating to age or meaning; something relating to word length and orthographic similarity; and maybe some thing relating to sublexical unit frequency. However, as noted previously, Cohen et al. (2003) provide good arguments for being cautious about performing a principal components regression in response to a state of high collinearity among your predictors, including problems relating to the interpretability of findings.

Center variables on their means

One perhaps partial means to alleviate the collinearity indicated may be to center predictor variables on their means.

(Should you center variables on their means before or after you remove errors, i.e. means calculated for the full or the no-errors dataframe? Should you center both predictors and the outcome variables? I will need to come back to those questions.)

Centering variables is helpful, also, for the interpretation of effects where 0 on the raw variables is not meaningful e.g. noone has an age of 0 years, no word has a length of 0 letters. With centered variables, if there is an effect then one can say that for unit increase in the predictor variable (where 0 for the variable is now equal to the mean for the sample, because of centering), there is a change in the outcome, on average, equal to the coefficient estimated for the effect.

Centering variables is helpful, especially, when we are dealing with interactions. Cohen et al. (2003) note that the collinearity between predictors and interaction terms is reduced (this is reduction of nonessential collinearity, due to scaling) if predictors are centered. Note that interactions are represented by the multiplicative product of their component variables. You will often see an interaction represented as “age x word length effects”, the “x” reflects the fact that for the interaction of age by length effects the interaction term is entered in the analysis as the product of the age and length variables. In addition, centering again helps with the interpretation of effects because if an interaction is significant then one must interpret the effect of one variable in the interaction while taking into account the other variable (or variables) involved in the interaction (Cohen et al., 2003; see, also, Gelman & Hill, 2007). As that is the case, if we center our variables and the interaction as well as the main effects are significant, say, in our example, the age, length and age x length effects, then we might look at the age effect and interpret it by reporting that for unit change in age the effect is equal to the coefficient while the effect of length is held constant (i.e. at 0, its mean).

As you would expect, you can center variables in R very easily, we will use one method, which is to employ the scale() function, specifying that we want variables to be centered on their means, and that we want the results of that operation to be added to the dataframe as centered variables. Note that by centering on their means, I mean we take the mean for a variable and subtract it from each value observed for that variable. We could center variables by standardizing them, where we both subtract the mean and divide the variable by its standard deviation (see Gelman & Hill’s 2007, recommendations) but we will look at that another time.

So, I center variables on their means, creating new predictor variables that get added to the dataframe with the following code:

# we might center the variables - looking ahead to the use of interaction terms - as the centering will
# both reduce nonessential collinearity due to scaling (Cohen et al., 2003) and help in the interpretation
# of effects (Cohen et al., 2003; Gelman & Hill, 2007 p .55) ie if an interaction is sig one term will be
# interpreted in terms of the difference due to unit change in the corresponding variable while the other is 0

nomissing.full$cLength <- scale(nomissing.full$Length, center = TRUE, scale = FALSE)
nomissing.full$cBG_Mean <- scale(nomissing.full$BG_Mean, center = TRUE, scale = FALSE)
nomissing.full$cOLD <- scale(nomissing.full$OLD, center = TRUE, scale = FALSE)
nomissing.full$cIMG <- scale(nomissing.full$brookesIMG, center = TRUE, scale = FALSE)
nomissing.full$cAOA <- scale(nomissing.full$AoA_Kup_lem, center = TRUE, scale = FALSE)
nomissing.full$cLgSUBTLCD <- scale(nomissing.full$LgSUBTLCD, center = TRUE, scale = FALSE)

nomissing.full$cAge <- scale(nomissing.full$Age, center = TRUE, scale = FALSE)
nomissing.full$cTOWREW <- scale(nomissing.full$TOWRE_wordacc, center = TRUE, scale = FALSE)
nomissing.full$cTOWRENW <- scale(nomissing.full$TOWRE_nonwordacc, center = TRUE, scale = FALSE)
nomissing.full$cART <- scale(nomissing.full$ART_HRminusFR, center = TRUE, scale = FALSE)

# subset the predictors again by items and person level attributes to make the plotting more sensible

nomissing.full.c.items <- subset(nomissing.full, select = c(

 "cLength", "cOLD", "cBG_Mean", "cLgSUBTLCD", "cIMG", "cAOA"

))

nomissing.full.c.subjects <- subset(nomissing.full, select = c(

 "cAge", "cTOWREW", "cTOWRENW", "cART"

))

# assess collinearity using the condition number, kappa, metric

collin.fnc(nomissing.full.c.items)$cnumber
collin.fnc(nomissing.full.c.subjects)$cnumber

# > collin.fnc(nomissing.full.c.items)$cnumber
# [1] 3.180112
# > collin.fnc(nomissing.full.c.subjects)$cnumber
# [1] 2.933563

Notice:

— I check the condition numbers for the predictors after centering and it appears that they are significantly reduced.

— I am not sure that that reduction can possibly be the end of the collinearity issue, but I shall take that result and run with it, for now.

— I also think that it would be appropriate to examine collinearity with both the centered variables and the interactions involving those predictors but that, too, can be left for another time.

Run the models

What I will do next is perform three sets of mixed-effects model analyses. I will talk about the first set in this post.

In this first set, I shall compare models varying in the predictor variables included in the model specification. We shall say that models with more predictors are more complex than models with fewer predictors (a subset of the predictors specified for the more complex models).

I shall then compare models of differing in complexity to see if increased complexity is justified by improved fit to data.

This is in response to: 1. reading Baayen (2008) and Pinheiro & Bates (2000) 2. recommendations by a reviewer; though I note that the reviewer recommendations are, in their application, qualified in my mind by some cautionary comments made by Pinheiro & Bates (2000), and confess that any problems of application or understanding are surely expressions of my misunderstanding.

What I am concerned about is the level of complexity that can be justified in the ultimate model by the contribution to improved fit by the model of the observed data. Of course, I have collected a set of predictors guided by theory, custom and practice in my field. But, as you have seen, I might choose to draw on a large set of potential predictors. I know that one cannot – to take one option used widely by psycholinguistics researchers – simply inspect a correlation table, comparing predictors with the outcome variable, and exclude those predictors that do not correlate with the outcome. Harrell (2001) comments that that approach has a biasing effect on the likelihood of detecting an effect that is really there (consuming, ‘ghost degrees of freedom’, or something like that). So what should we do or how should we satisfy ourselves that we should or should not include one or more predictor variables in our models?

You could start complex and step backwards to the simplest model that appears justified by model fit to observed data. I will return to that option another time.

In this post, I will start with the simplest model and build complexity up. Simpler models can be said to be nested in more complex models, e.g. a simple model including just main effects vs. a more complex model also including interactions. I will add complexity by adding sets of predictors, and I will compare each proximate pair of simple model and more complex model using the Likelihood Ratio Test (Pinheiro & Bates, 2000; see, especially, chapter 2, pp. 75-).

We can compare models with the same random effects (e.g. of subjects or items) but varying in complexity with respect to the fixed effects, i.e. replicable or manipulated variables like item length or participant age, and, separately, models with the same fixed effects but varying random effects.

Note that in comparing models varying in random effects, one estimates those effects using restricted maximum likelihood: you will see the argument REML = TRUE in the lmer() function call, that is what REML means. Note that in comparing models varying in fixed effects one must estimate those effects using maximum likelihood: you will see the argument REML = FALSE in the lmer() function call, that is what FALSE means. See comments in Baayen (2008) and Pinheiro & Bates (2000); I will come back to those important terms to focus on understanding, another time, focusing in this post on just writing the code for running the models.

We can compare the more and less complex models using the Likelihood Ration Test (LRT) which is executed with the anova([simple model], [more complex model]) function call. A statistic is computed, and evaluated against the  distribution to estimate the probability of an increase in model likelihood as large or larger as that observed when comparing the more or less complex model, given the null hypothesis of no gain in likelihood.

Note that I log transform the RTs but one might also consider examining the reciprocal RT.

# we can move to some multilevel modelling ###############################################################

# we might start by examining the effects of predictors in a series of additions of sets of predictors
# we can hold the random effects, of subjects and items, constant, while varying the fixed effects
# we can compare the relative fit of models to data using the anova() likelihood ratio test
# in this series of models, we will use ML fitting

full.lmer0 <- lmer(log(RT) ~

# Trial.order +
#
# cAge + cTOWREW + cTOWRENW + cART +
#
# cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG +

 (1|subjectID) + (1|item_name),

 data = nomissing.full, REML = FALSE)

print(full.lmer0,corr=F)

#

full.lmer1 <- lmer(log(RT) ~

 Trial.order +

 # cAge + cTOWREW + cTOWRENW + cART +
 #
 # cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG +

 (1|subjectID) + (1|item_name),

 data = nomissing.full, REML = FALSE)

print(full.lmer1,corr=F)

#

full.lmer2 <- lmer(log(RT) ~

 Trial.order +

 cAge + cTOWREW + cTOWRENW + cART +

 # cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG +

 (1|subjectID) + (1|item_name),

 data = nomissing.full, REML = FALSE)

print(full.lmer2,corr=F)

#

full.lmer3 <- lmer(log(RT) ~

 Trial.order +

 cAge + cTOWREW + cTOWRENW + cART +

 cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG +

 (1|subjectID) + (1|item_name),

 data = nomissing.full, REML = FALSE)

print(full.lmer3,corr=F)

#

full.lmer4 <- lmer(log(RT) ~

 Trial.order +

 (cAge + cTOWREW + cTOWRENW + cART)*

 (cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG) +

 (1|subjectID) + (1|item_name),

 data = nomissing.full, REML = FALSE)

print(full.lmer4,corr=F)

# compare models of varying complexity

anova(full.lmer0, full.lmer1)
anova(full.lmer1, full.lmer2)
anova(full.lmer2, full.lmer3)
anova(full.lmer3, full.lmer4)

This code will first print out the summaries of each model, along the lines you have already seen. It will then give you this:

# > # compare models of varying complexity
# >
# > anova(full.lmer0, full.lmer1)
# Data: nomissing.full
# Models:
# full.lmer0: log(RT) ~ (1 | subjectID) + (1 | item_name)
# full.lmer1: log(RT) ~ Trial.order + (1 | subjectID) + (1 | item_name)
# Df AIC BIC logLik Chisq Chi Df Pr(>Chisq)
# full.lmer0 4 -977.58 -951.31 492.79
# full.lmer1 5 -975.83 -943.00 492.92 0.2545 1 0.6139
# > anova(full.lmer1, full.lmer2)
# Data: nomissing.full
# Models:
# full.lmer1: log(RT) ~ Trial.order + (1 | subjectID) + (1 | item_name)
# full.lmer2: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + (1 |
# full.lmer2: subjectID) + (1 | item_name)
# Df AIC BIC logLik Chisq Chi Df Pr(>Chisq)
# full.lmer1 5 -975.83 -943.00 492.92
# full.lmer2 9 -977.09 -917.98 497.54 9.2541 4 0.05505 .
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# > anova(full.lmer2, full.lmer3)
# Data: nomissing.full
# Models:
# full.lmer2: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + (1 |
# full.lmer2: subjectID) + (1 | item_name)
# full.lmer3: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + cLength +
# full.lmer3: cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1 | subjectID) +
# full.lmer3: (1 | item_name)
# Df AIC BIC logLik Chisq Chi Df Pr(>Chisq)
# full.lmer2 9 -977.09 -917.98 497.54
# full.lmer3 15 -1115.42 -1016.91 572.71 150.34 6 < 2.2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# > anova(full.lmer3, full.lmer4)
# Data: nomissing.full
# Models:
# full.lmer3: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + cLength +
# full.lmer3: cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1 | subjectID) +
# full.lmer3: (1 | item_name)
# full.lmer4: log(RT) ~ Trial.order + (cAge + cTOWREW + cTOWRENW + cART) *
# full.lmer4: (cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG) +
# full.lmer4: (1 | subjectID) + (1 | item_name)
# Df AIC BIC logLik Chisq Chi Df Pr(>Chisq)
# full.lmer3 15 -1115.4 -1016.91 572.71
# full.lmer4 39 -1125.7 -869.56 601.84 58.262 24 0.0001119 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# it looks like the full model, including interactions but not the trialorder variable, is justified

Notice:

— It is not very pretty but it does tell you what predictors are included in each model you are comparing, for each pair of models being compared, the outcome of the ratio test, giving the numbers I usually report: the and the .

— I am looking at this output to see if, for each pair of models, the more complex model fits the data significantly better (if p =< 0.05).

–I add predictors in blocks and assess the improvement of fit associated with the whole block.

I have made a lot of promises to explain things more another time. So I will add one more. Pinheiro & Bates (2000; p. 88) argue that Likelihood Ratio Test comparisons of models varying in fixed effects tend to be anticonservative i.e. will see you observe significant differences in model fit more often than you should. I think they are talking, especially, about situations in which the number of model parameter differences (differences between the complex model and the nested simpler model) is large relative to the number of observations. This is not really a worry for this dataset, but I will come back to the substance of this view, and alternatives to the approach taken here.

What next?

What I would seek to do in the next series of analyses is determine if the effects that are significant appear to be significant due:

1. to the presence of other, nonsignificant effects — making the check by removing the nonsignificant effects then rerunning the model;

2. to the presence of outlier observations — making the check by removing observations associated with large model residuals then rerunning the model.

What have we learnt?

(The code I have used in running the analysis described in this post can be found here.)

Firstly, I am going to have to do a lot more explaining, for my own sake, and have promised to do so for a wide range of ideas, including those concerning the methods of model fitting, and, especially, the discussion around how one determines the appropriate set of fixed effects.

Secondly, that the model code is both simple and – on its face – reasonably intuitive.

Key vocabulary (mostly, a list of things to be explained)

fixed effects

random effects

random intercepts

random slopes

interactions

multiplicative products

centering

maximum likelihood

restricted maximum likelihood

Markov chain Monte Carlo

Likelihood Ratio Test

lmer()

anova()

Reading

Baayen, R. H. (2008). Analyzing linguistic data. Cambridge University Press.
Bates, D. M. (2005). Fitting linear mixed models in R. R News, 5, 27-30.
Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. New York: Wiley.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioural sciences (3rd. edition). Mahwah, NJ: Lawrence Erlbaum Associates.
Gelman, A., & Hill, J. (2007). Data analysis using regression and multilevel/hierarchical models. New York,NY: Cambridge University Press.
Pinheiro, J. C., & Bates, D. M. (2000). Mixed-effects models in S and S-plus (Statistics and Computing). New York: Springer.

Watching someone else do or talk about computing is boring, as many rubbish and one good film of the past have proved.

Still from WarGames (1983), source: imdb

Better to do something practical and, here, the task is to evaluate if R is something you want or need to learn or not. Thus, this practical session is designed to show that:

1. It is easy to download and install R along with R-Studio, the interface you might use to work with R.

2. It is easy and efficient to load in and work with R.

3. Performing analyses makes intuitive sense.

4. Visualizing your data is way more effective than anywhere else – the plots are prettier and more informative.

In case you’re interested, I’ve got a more drawn out exposition of this point, see “Browse by category” menu, starting here:

https://ayeimanol-r.net/2013/04/13/getting-started-in-r/

Installation – R

How do you download and install R? Google “CRAN” and click on the download link, then follow the instructions (e.g. at “install R for the first time”).

Obviously, you will require administration rights though I believe you can download the installation file (.dmg in Mac) run it and then stick the application in your applications folder without the ned for full admin rights.

What you’ll get is the R statistical computing environment and you can work with R through the console. I find it easier to use the R-Studio interface, for reasons I’ll explain.

Installation – RStudio

I am repeating this post in summary:

https://ayeimanol-r.net/2013/04/21/289/

If you google “R-studio” you will get to this window:

Click on the “Download now” button and you will see this window:

Click on the “Download RStudio desktop” and you will see this window:

You can just click on the link to the installer recommended for your computer.

What happens next depends on whether you have administrative/root privileges on your computer.

I believe you can install R-studio without such rights using the zip/tarball dowload.

Having installed R and R-studio…

— in Windows you will see these applications now listed as newly installed programs at the start menu. Depending on what you said in the installation process, you might also have icons on your desktop.

— in Mac you should see RStudio in your applications folder and launchpad.

Click on the R-studio icon – it will pick up the R installation for you.

Now we are ready to get things done in R.

Start a new script in R-studio, install packages, draw a plot

Here, we are going to 1. start a new script, 2. install then load a library of functions (ggplot2) and 3. use it to draw a plot.

Depending on what you did at installation, you can expect to find shortcut links to R (a blue R) and to R-Studio (a shiny blue circle with an R) in the Windows start menu, or as icons on the desktop.

To get started, in Windows, double click (left mouse button) on the R-Studio icon.

Maybe you’re now looking at this:

1. Start a new script

What you will need to do next is go to the file menu [top left of R-Studio window] and create a new R script:

–move the cursor to file – then – new – then – R script and then click on the left mouse button

or

— just press the buttons ctrl-shift-N at the same time — the second move is a keyboard shortcut for the first, I prefer keyboard short cuts to mouse moves

— to get this:

What’s next?

This circled bit you see in the picture below:

is the console.

It is what you would see if you open R directly, not using R-Studio.

You can type and execute commands in it but mostly you will see unfolding here what happens when you write and execute commands in the script window, circled below:

— The console reflects your actions in the script window.

If you look on the top right of the R-Studio window, you can see two tabs, Workspace and History: these windows (they can be resized by dragging their edges) also reflect what you do:

1. Workspace will show you the functions, data files and other objects (e.g. plots, models) that you are creating in your R session.

[Workspace — See the R introduction, and see the  this helpful post by Quick-R — when you work with R, your commands result in the creation of objects e.g. variables or functions, and during an R session these objects are created and stored by name — the collection of objects currently stored is the workspace.]

2. History shows you the commands you execute as you execute them.

— I look at the Workspace a lot when using R-Studio, and no longer look at (but did once use) History much.

My script is my history.

2. Install then load a library of functions (ggplot2)

We can start by adding some capacity to the version of R we have installed. We install packages of functions that we will be using e.g. packages for drawing plots (ggplot2) or for modelling data (lme4).

[Packages – see the introduction and this helpful page in Quick-R — all R functions and (built-in) datasets are stored in packages, only when a package is loaded are its contents available]

Copy then paste the following command into the script window in R-studio:

install.packages("ggplot2", "reshape2", "plyr", "languageR",
"lme4", "psych")

Highlight the command in the script window …

— to highlight the command, hold down the left mouse button, drag the cursor from the start to the finish of the command

— then either press the run button …

[see the run button on the top right of the script window]

… or press the buttons CTRL-enter together, and watch the console show you R installing the packages you have requested.

Those packages will always be available to you, every time you open R-Studio, provided you load them at the start of your session.

[I am sure there is a way to ensure they are always loaded at the start of the session and will update this when I find that out.]

There is a 2-minute version of the foregoing laborious step-by-step, by ajdamico, here. N.B. the video is for installing and loading packages using the plain R console but applies equally to R-Studio.

Having installed the packages, in the same session or in the next session, the first thing you need to do is load the packages for use by using the library() function:

library(languageR)
library(lme4)
library(ggplot2)
library(rms)
library(plyr)
library(reshape2)
library(psych)

— copy/paste or type these commands into the script, highlight and run them: you will see the console fill up with information about how the packages are being loaded:

Notice that the packages window on the bottom right of R-Studio now shows the list of packages have been ticked:

Let’s do something interesting now.

3. Use ggplot function to draw a plot

[In the following, I will use a simple example from the ggplot2 documentation on geom_point.]

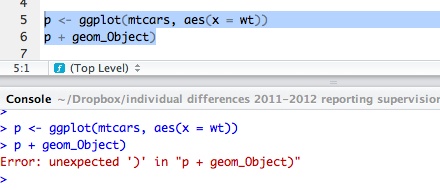
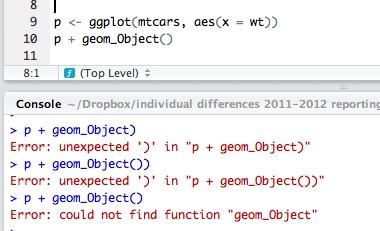
Copy the following two lines of code into the script window:

p <- ggplot(mtcars, aes(wt, mpg))
p + geom_point()

— run them and you will see this:

— notice that the plot window, bottom right, shows you a scatterplot.

How did this happen?

Look at the first line of code:

p <- ggplot(mtcars, aes(wt, mpg))

— it creates an object, you can see it listed in the workspace (it was not there before):

— that line of code does a number of things, so I will break it down piece by piece:

p <- ggplot(mtcars, aes(wt, mpg))

p <- ...

— means: create <- (assignment arrow) an object (named p, now in the workspace)

... ggplot( ... )

— means do this using the ggplot() function, which is provided by installing the ggplot2 package then loading (library(ggplot) the ggplot2 package of data and functions

... ggplot(mtcars ...)

— means create the plot using the data in the database (in R: dataframe) called mtcars

— mtcars is a dataframe that gets loaded together with functions like ggplot when you execute: library(ggplot2)

... ggplot( ... aes(wt, mpg))

— aes(wt,mpg) means: map the variables wt and mpg to the aesthetic attributes of the plot.

In the ggplot2 book (Wickham, 2009, e.g. pp 12-), the things you see in a plot, the colour, size and shape of the points in a scatterplot, for example, are aesthetic attributes or visual properties.

— with aes(wt, mpg) we are informing R(ggplot) that the named variables are the ones to be used to create the plot.

Now, what happens next concerns the nature of the plot we want to produce: a scatterplot representing how, for the data we are using, values on one variable relate to values on the other.

A scatterplot represents each observation as a point, positioned according to the value of two variables. As well as a horizontal and a vertical position, each point also has a size, a colour and a shape. These attributes are called aesthetics, and are the properties that can be perceived on the graphic.

(Wickham: ggplot2 book, p.29; emphasis in text)

— The observations in the mtcars database are information about cars, including weight (wt) and miles per gallon (mpg).

[see

http://127.0.0.1:29609/help/library/datasets/html/mtcars.html

in case you’re interested]

— This bit of the code asked the p object to include two attributes: wt and mpg.

— The aesthetics (aes) of the graphic object will be mapped to these variables.

— Nothing is seen yet, though the object now exists, until you run the next line of code.

The next line of code:

p + geom_point()

— adds (+) a layer to the plot, a geometric object: geom

— here we are asking for the addition of geom_point(), a scatterplot of points

— the variables mpg and wt will be mapped to the aesthetics, x-axis and y-axis position, of the scatterplot

The wonderful thing about the ggplot() function is that we can keep adding geoms to modify the plot.

— add a command to the second line of code to show the relationship between wt and mpg for the cars in the mtcars dataframe:

p <- ggplot(mtcars, aes(wt, mpg))
p + geom_point() + geom_smooth()

— here

+ geom_smooth()

adds a loess smoother to the plot, indicating the predicted miles per gallon (mpg) for cars, given the data in mtcars, given a car’s weight (wt).

[If you want to know what loess means – this post looks like a good place to get started.]

Notice that there is an export button on the top of the plots window pane, click on it and export the plot as a pdf.

Where does that pdf get saved to? Good question.

Extras

The really cool thing about drawing plots in R (if using ggplot2, especially) is that one can modify plots towards a target utility intuitively, over  a series of steps:

So far, we have mapped car weight (wt) and miles per gallon (mpg) in the mtcars database to the x and y coordinates of the plot. Is there more in the data that we can bring out in the visualization?

You can check out what is in the database:

# what is in this database?

help(mtcars)

View(mtcars)

Maybe we want to bring the power of the cars into the picture because, presumably, heavier cars consume more petrol because they need to have more power (you tell me).

We can add power (hp) to the set of aesthetics and map it to further plot attributes e.g. colour or size:

# maybe it would be interesting to add information to the plot about
# horsepower

p <- ggplot(mtcars, aes(x = wt, y = mpg, colour = hp))
p + geom_point()

# maybe it would be interesting to add information to the plot about
# horsepower

p <- ggplot(mtcars, aes(x = wt, y = mpg, size = hp))
p + geom_point()

Next, I would like to edit the plot a bit for presentation:

i. add in a smoother but the wiggliness of the loess is not helping much;

ii. add a plot title and relabel the axes to make them more intelligible;

ii. modify the axis labelling because the labels are currently too small for a presentation;

iv. make the background white.

— of course, this is going to be easy and do-able in steps, as follows.

Notice that I change the format of the coding a little bit to make it easier to keep track of the changes.

# add the smoother back in, I don't think the wiggliness of the default loess helps much so modify the line fitting method

p <- ggplot(mtcars, aes(x = wt, y = mpg, size = hp, colour = hp))
p + geom_point() + geom_smooth(method = "lm")

# add a plot title and make the axis labels intelligible

p <- ggplot(mtcars, aes(x = wt, y = mpg, colour = hp, size = hp))
p <- p + geom_point() + geom_smooth(method = "lm") + labs(title = "Cars plot")
p <- p + xlab("Vehicle Weight") + ylab("Miles per Gallon")
p

# modify the label sizing -- modify sizes plot title, axis labels, axis tick value labels

p <- ggplot(mtcars, aes(x = wt, y = mpg, colour = hp, size = hp))
p <- p + geom_point() + geom_smooth(method = "lm") + labs(title = "Cars plot")
p <- p + xlab("Vehicle Weight") + ylab("Miles per Gallon")
p <- p + theme(plot.title = element_text(size = 80))
p <- p + theme(axis.text = element_text(size = 35))
p <- p + theme(axis.title.y = element_text(size = 45))
p <- p + theme(axis.title.x = element_text(size = 45))
p

# change the background so the plot is on white

p <- ggplot(mtcars, aes(x = wt, y = mpg, colour = hp, size = hp))
p <- p + geom_point() + geom_smooth(method = "lm") + labs(title = "Cars plot")
p <- p + xlab("Vehicle Weight") + ylab("Miles per Gallon")
p <- p + theme(plot.title = element_text(size = 80))
p <- p + theme(axis.text = element_text(size = 35))
p <- p + theme(axis.title.y = element_text(size = 45))
p <- p + theme(axis.title.x = element_text(size = 45))
p <- p + theme_bw()
p

On reflection, you might ask what we are adding by putting in colour and size modification to depict horse power. Decisions will be more sensible if we start using some real data.

Getting your data into R

Just as in other statistics applications e.g. SPSS, data can be entered manually, or imported from an external source. Here I will talk about: 1. loading files into the R workspace as dataframe object; 2. getting summary statistics for the variables in the dataframe; 3. and plotting visualizations of pairwise relationships in the data.

1. Loading files into the R workspace as dataframe object

Start by getting your data files

I often do data collection using paper-and-pencil standardized tests of reading ability and also DMDX scripts running e.g. a lexical decision task testing online visual word recognition. Typically, I end up with an excel spreadsheet file called subject scores 210413.xlsx and a DMDX output data file called lexical decision experiment 210413.azk. I’ll talk about the experimental data collection data files another time.

The paper and pencil stuff gets entered into the subject scores database by hand. Usually, the spreadsheets come with notes to myself on what was happening during testing. To prepare for analysis, though, I will often want just a spreadsheet showing columns and rows  of data, where the columns are named sensibly (meaningful names, I can understand) with no spaces in either column names or in entries in data cells. Something that looks like this:

This is a screen shot of a file called: ML scores 080612 220413.csv

— which you can download here.

These data were collected in an experimental study of reading, the ML study.

The file is in .csv (comma separated values) format. I find this format easy to use in my workflow –collect data–tidy in excel–output to csv–read into R–analyse in R, but you can get any kind of data you can think of into R (SPSS .sav or .dat, .xlsx, stuff from the internet — no problem).

Let’s assume you’ve just downloaded the database and, in Windows, it has ended up in your downloads folder. I will make life easier for myself by copying the file into a folder whose location I know.

— I know that sounds simple but I often work with collaborators who do not know where their files are.

Read a data file into the R workspace

I have talked about the workspace before, here we are getting to load data into it using the functions setwd() and read.csv().

In R, you need to tell it where your data can be found, and where to put the outputs (e.g. pdfs of a plot). You need to tell it the working directory (see my advice earlier about folders): this is going to be the Windows folder where you put the data you wish to analyse.

For this example, the folder is:

C:\Users\p0075152\Dropbox\resources R public

[Do you know what this is – I mean, the equivalent, on your computer? If not, see the video above – or get a Windows for Dummies book or the like.]

What does R think the working directory currently is? You can find out, run the getwd() command:

getwd()

and you will likely get told this:

> getwd()
[1] “/Users/robdavies”

— with a different username, obviously.

The username folder is not where the data file is, so you set the working directory using setwd()

setwd("/Users/robdavies/Downloads")

— you need to:

— find the file in your downloads folder

— highlight the file in Mac Finder and use the Finder file menu getinfo option for the file to find the path to it

— copy that path information into the setwd() function call and run it

— typical errors include misspelling elements of the path, not putting it in “”

Load the data file using the read.csv() function

subjects <- read.csv("ML scores 080612 220413.csv", header=T, na.strings = "-999")

Notice:

1. subjects… — I am calling the dataframe something sensible

2. …<- read.csv(…) — this is the part of the code loading the file into the workspace

3. …(“ML scores 080612 220413.csv”…) — the file has to be named, spelled correctly, and have the .csv suffix given

4. …, header = T… — I am asking for the column names to be included in the subjects dataframe resulting from this function call

5. … na.strings = “-999” … — I am asking R to code -999 values, where they are found, as NA – in R, NA means Not Available i.e. a missing value.

Things that can go wrong here:

— you did not set the working directory to the folder where the file is

— you misspelled the file name

— either error will cause R to tell you the file does not exist (it does, just not where you said it was)

I recommend you try making these errors and getting the error message deliberately. Making errors is a good thing in R.

Note:

— coding missing values systematically is a good thing -999 works for me because it never occurs in real life for my reading experiments

— you can code for missing values in excel in the csv before you get to this stage

Let’s assume you did the command correctly, what do you see? This:

Notice:

1. in the workspace window, you can see the dataframe object, subjects, you have now created

2. in the console window, you can see the commands executed

3. in the script window, you can see the code used

4. the file name, top of the script window, went from black to red, showing a change has been made but not yet saved.

To save a change, keyboard shortcut is CTRL-S.

2. Getting summary statistics for the variables in the dataframe

It is worth reminding ourselves that R is, among other things, an object-oriented programming language. See this:

The entities that R creates and manipulates are known as objects. These may be variables, arrays of numbers, character strings, functions, or more general structures built from such components.

During an R session, objects are created and stored by name (we discuss this process in the next session). The R command

     > objects()

(alternatively, ls()) can be used to display the names of (most of) the objects which are currently stored within R. The collection of objects currently stored is called the workspace.

[R introduction: http://cran.r-project.org/doc/manuals/r-release/R-intro.html#Data-permanency-and-removing-objects]

or this helpful video by ajdamico.

So, we have created an object using the read.csv() function. We know that object was a .csv file holding subject scores data. In R, in the workspace, it is an object that is a dataframe, a structure much like the spreadsheets in excel, SPSS etc.: columns are variables and  rows are observations, with columns that can correspond to variables of different types (e.g. factors, numbers etc.) Most of the time, we’ll be using dataframes in our analyses.

You can view the dataframe by running the command:

view(subjects)

— or actually just clicking on the name of the dataframe in the workspace window in R-studio, to see:

Note: you cannot edit the file in that window, try it.

Now that we have created an object, we can interrogate it. We can ask what columns are in the subjects dataframe, how many variables there are, what the average values of the variables are, if there are missing values, and so on using an array of useful functions:

head(subjects, n = 2)

summary(subjects)

describe(subjects)

str(subjects)

psych::describe(subjects)

length(subjects)

length(subjects$Age)

Copy-paste these commands into the script window and run them, below is what you will see in the console:

Notice:

1. the head() function gives you the top rows, showing column names and data in cells; I asked for 2 rows of data with n = 2

2. the summary() function gives you: minimum, maximum, median and quartile values for numeric variables, numbers of observations with one or other levels for factors, and will tell you if there are any missing values, NAs

3. describe() (from the psych package) will give you means, SDs, the kind of thing you report in tables in articles

4. str() will tell you if variables are factors, integers etc.

If I were writing a report on this subjects data I would copy the output from describe() into excel, format it for APA, and stick it in a word document.

3. Plotting visualization of data and doing a little bit of modelling

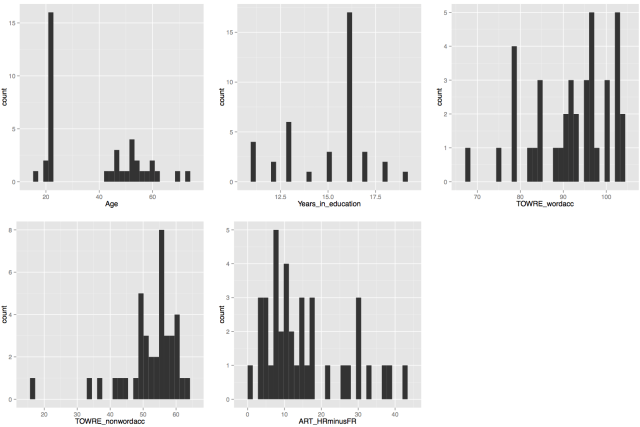
In a previous post, I went into how you can plot histograms of the data to examine the distribution of the variables, see here:

https://ayeimanol-r.net/2013/04/22/getting-started-working-directories-loading-data-and-a-bit-more-plotting/

but for this post I want to stick to the focus on relationships between variables.

Let’s use what we learnt to examine visually the relationships between variables in the dataset. Here, our concern might be whether measures of reading performance, collected using the TOWRE (Torgesen et al., 1998) a test of word and non-word accuracy where participants are asked to read lists of words or non-words, of increasing difficulty, in 45 s, and the performance score is the number of words read correctly in that time.

I might expect to see that the ability to read aloud words correctly actually increases as: 1. people get older – increased word naming accuracy with increased age; 2. people read more – increased word naming accuracy with increased reading history (ART score); 3. people show increased ability to read aloud made-up words (pseudowords) or nonwords – increased word naming accuracy with increased nonword naming accuracy.

We can examine these relationships and, in this post, we will work on doing so through using scatter plots like that shown below.

What does the scatterplot tell us, and how can it be made?

Notice:

— if people are more accurate on nonword reading they are also often more accurate on word reading

— at least one person is very bad on nonword reading but OK on word reading

— most of the data we have for this group of ostensibly typically developing readers is up in the good nonword readers and good word readers zone.

I imposed a line of best fit indicating the relationship between nonword and word reading estimated using linear regression, the line in blue, as well as a shaded band to show uncertainty – confidence interval – over the relationship. You can see that the uncertainty increases as we go towards low accuracy scores on either measure. We will return to these key concepts in other posts.

For now, we will stick to showing the relationships between all the variables in our sample, modifying plots over a series of steps as follows:

[In what follows, I will be using the ggplot2 documentation that can be found online, and working my way through some of the options discussed in Winston Chang’s book: R Graphics Cookbook .]

Draw a scatterplot using default options

Let’s draw a scatterplot using geom_point(). Run the following line of code

ggplot(subjects, aes(x = Age, y = TOWRE_wordacc)) + geom_point()

and you should see this in R-studio Plots window:

Notice:

— There might be no relationship between age and reading ability: how does ability vary with age here?

— Maybe the few older people, in their 60s, pull the relationship towards the negative i.e. as people get older abilities decrease.

Let’s imagine that we wanted to report a plot showing the relationship between word and nonword reading. We can modify the plot for presentation as we have done previously but we also add modifications to the axis labelling — fixing the axis limits and reducing the number of ticks to tidy the plot a bit.

# generate a scatterplot showing the relationship between a pair of variables
# let's split the plot construction into two sets of steps:

pNW <- ggplot(subjects,aes(x=TOWRE_nonwordacc, y=TOWRE_wordacc))
pNW <- pNW + geom_point() + ylim(70, 104)
pNW <- pNW + scale_x_continuous(breaks = c(20, 40, 60))
pNW <- pNW + geom_smooth(method="lm", size = 1.5)
pNW <- pNW + theme_bw()
pNW

pNW <- pNW + ggtitle("Word vs. nonword reading
skill")
pNW <- pNW + xlab("TOWRE nonword naming accuracy") + ylab("TOWRE word naming accuracy")
pNW <- pNW + theme(plot.title = element_text(size = 40))
pNW <- pNW + theme(axis.text = element_text(size = 25))
pNW <- pNW + theme(axis.title.y = element_text(size = 30))
pNW <- pNW + theme(axis.title.x = element_text(size = 30))
pNW

Notice:

— I am adding each change, one at a time, making for more lines of code; but I could and will be more succinct.

— I  add the title with: + ggtitle(“Word vs. nonword reading skill”)

— I change the axis labels with: + xlab(“TOWRE nonword naming accuracy”) + ylab(“TOWRE word naming accuracy”) 

— I fix the y-axis limits with: + ylim(70, 104)

— I change where the tick marks on the x-axis are with: + scale_x_continuous(breaks = c(20, 40, 60)) — there were too many before

— I modify the size of the axis labels for better readability with: + theme(axis.title.x = element_text(size=25), axis.text.x = element_text(size=20))

— I add a smoother i.e. a line showing a linear model prediction of y-axis values for the x-axis variable values with: + geom_smooth(method=”lm”, size = 1.5)  — and I ask for the size to be increased for better readability

— And then I ask for the plot to have a white background with: + theme_bw()

All that will get you this:

A bit of modelling

Can we get some stats in here now?

You will have started to see signs about one feature of R: there are multiple different ways to do a thing. That’s also true of what we are going to do next and last, a regression model of the ML subject scores data to look at the predictors of word reading accuracy. We are going to use the lm() function call, it’s simple, but we could use ols().

# generate a scatterplot showing the relationship between a pair of variables
# let's split the plot construction into two sets of steps:

# let's do a little bit of regresion modeling

help(lm)

summary(subjects)

MLwords.lm <- lm(TOWRE_wordacc ~

Age + TOWRE_nonwordacc + ART_HRminusFR,

data = subjects)

summary(MLwords.lm)

Notice:

— The code specifying the model is written to produce a regression object

MLwords.lm <- lm(TOWRE_wordacc ~

Age + TOWRE_nonwordacc + ART_HRminusFR,

data = subjects)

— Run it and you will see a model object appear in the workspace window, top right of RStudio but you will only see the code being repeated in the console.

— R will only show you what you ask for.

— The model formula is written out the same way you might write a regression equation i.e. the code syntax matches the statistical formula convention. Obviously, this is not an accident.

— Looking ahead, specifying models for ANOVA, mixed effects models etc. all follow the same sort of structure — the code syntax matches the conceptual unity.

Running this code will get you:

Thus, we see the same statistical output we would see anywhere else.

What have we learnt?

— starting a new script

— installing and loading packages

— creating a new plot

Vocabulary

functions

install.packages()

library()

ggplot()

critical terms

object

workspace

package

scatterplot

loess

aesthetics

Resources

You can download the .R code I used for the class here.

There is a lot more that you can do with plotting than I have shown here, see the technical help with examples you can run just by copying them into RStudio, here:

http://docs.ggplot2.org/current/

There’s a nice tutorial here:

http://www.r-bloggers.com/ggplot2-tutorial/

Reading

Baayen, R. H. (2008). Analyzing linguistic data. Cambridge University Press.
Castles, A., & Nation, K. (2006). How does orthographic learning happen? In S. Andrews (Ed.), From inkmarks to ideas: Challenges and controversies about word recognition and reading. Psychology Press.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioural sciences (3rd. edition). Mahwah, NJ: Lawrence Erlbaum Associates.
Harm, M. W., & Seidenberg, M. S. (2004). Computing the meanings of words in reading: Cooperative division of labor between visual and phonological processes. Psychological Review, 111, 662-720.
Harrell Jr, F. J. (2001). Regression modelling strategies: With applications to linear models, logistic regression, survival analysis. New York, NY: Springer.
Masterson, J., & Hayes, M. (2007). Development and data for UK versions of an author and title recognition test for adults. Journal of Research in Reading, 30, 212-219.
Nation, K. (2008). Learning to read words. The Quarterly Journal of Experimental Psychology, 61, 1121-1133.
Rayner, K., Foorman, B. R., Perfetti, C. A., Pesetsky, D., & Seidenberg, M. S. (2001). How psychological science informs the teaching of reading. Psychological Science in the Public Interest, 2, 31-74.
Share, D. L. (1995). Phonological recoding and self-teaching: sine qua non of reading acquisition. Cognition, 55, 151-218.
Stanovich, K. E., & West, R. F. (1989). Exposure to print and orthographic processing. Reading Research Quarterly, 24, 402-433.
Torgesen, J. K., Wagner, R. K., & Rashotte, C. A. (1999). TOWRE Test of word reading efficiency. Austin,TX: Pro-ed.