In the previous post, we ran through an example of a mixed-effects analysis completed using the lmer() function from the lme4 package (Bates, 2005; Bates, Maelchler & Bolker, 2013).
We will not, yet, really fulfill the promise to develop our understanding but we will add snippets of vocabulary for the area that we shall return to later.
We are working, again, with the dataframe collated in previous posts (see here), which combines data about subject attributes, item attributes, and the observed behavioural responses (keypress responses in lexical decision) of the participants to a set of 160 words.
In this post, we will consider a more extended example. We will work through a series of models in a sequence to examine what fixed effects appear to improve the capacity of the model to fit the observed responses.
In following posts, we shall 1. perform some checks on whether the fixed effects appear justified with respect to data hygiene 2. examine what random effects seem justified, looking at random effects on intercepts and random effects on slopes.
We shall also consider how to produce partial effects plots depicting the effects i.e. the model predictions taking everything into account.
Note the terms in use in this area. People (e.g. Pinheiro & Bates, 2000) often refer to fixed effects as the effects on response variance due to variables that are manipulated (e.g. different conditions) or where variation can be replicated (e.g. presenting long vs. short words). They then refer to random effects as the effects on response variance corresponding to grouping units (e.g. subjects who all read some set of words) in sampling. Pinheiro & Bates (2000) explain that a mixed-effects model has both fixed effects and random effects. Some authors (e.g. Gelman & Hill, 2007) assert, as I understand it, that the distinction tends to break down if you put the idea under pressure.
As usual, we will work through a series of self-annotated phases.
Load libraries, define functions, load data
We start by loading the libraries of functions we are likely to need, defining a set of functions not in libraries, setting the working directory, and loading the dataframe we will work with into the R session workspace.
# load libraries of packages #############################################################################
library(languageR)
library(lme4)
library(ggplot2)
library(grid)
library(rms)
library(plyr)
library(reshape2)
library(psych)
library(gridExtra)
# define functions #######################################################################################
# pairs plot function
#code taken from part of a short guide to R
#Version of November 26, 2004
#William Revelle
# see: http://www.personality-project.org/r/r.graphics.html
panel.cor <- function(x, y, digits=2, prefix="", cex.cor)
{
usr <- par("usr"); on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r = (cor(x, y))
txt <- format(c(r, 0.123456789), digits=digits)[1]
txt <- paste(prefix, txt, sep="")
if(missing(cex.cor)) cex <- 0.8/strwidth(txt)
text(0.5, 0.5, txt, cex = cex * abs(r))
}
# just a correlation table, taken from here:
# http://myowelt.blogspot.com/2008/04/beautiful-correlation-tables-in-r.html
# actually adapted from prvious nabble thread:
corstarsl <- function(x){
require(Hmisc)
x <- as.matrix(x)
R <- rcorr(x)$r
p <- rcorr(x)$P
## define notions for significance levels; spacing is important.
mystars <- ifelse(p < .001, "***", ifelse(p < .01, "** ", ifelse(p < .05, "* ", " ")))
## trunctuate the matrix that holds the correlations to two decimal
R <- format(round(cbind(rep(-1.11, ncol(x)), R), 2))[,-1]
## build a new matrix that includes the correlations with their apropriate stars
Rnew <- matrix(paste(R, mystars, sep=""), ncol=ncol(x))
diag(Rnew) <- paste(diag(R), " ", sep="")
rownames(Rnew) <- colnames(x)
colnames(Rnew) <- paste(colnames(x), "", sep="")
## remove upper triangle
Rnew <- as.matrix(Rnew)
Rnew[upper.tri(Rnew, diag = TRUE)] <- ""
Rnew <- as.data.frame(Rnew)
## remove last column and return the matrix (which is now a data frame)
Rnew <- cbind(Rnew[1:length(Rnew)-1])
return(Rnew)
}
# read in data files #####################################################################################
getwd()
# set the working directory
setwd("C:/Users/p0075152/Dropbox/resources R public")
# read in the full database
RTs.norms.subjects <- read.csv("RTs.norms.subjects 090513.csv", header=T, na.strings = "-999")
If you run all that code, you will see the dataframes and functions appear listed in the workspace window of R-studio.
Prepare data – remove errors
As in the previous post, we need to remove errors from the dataframe. We can do this by setting a condition on rows, subsetting the dataframe to a new dataframe where no RT is less than zero because DMDX outputs .azk datafiles in which incorrect RTs are listed as negative numbers.
# preparing our dataframe for modelling ################################################################## # the summary shows us that there are negative RTs, which we can remove by subsetting the dataframe # by setting a condition on rows nomissing.full <- RTs.norms.subjects[RTs.norms.subjects$RT > 0,] # inspect the results summary(nomissing.full) # how many errors were logged? # the number of observations in the full database i.e. errors and correct responses is: length(RTs.norms.subjects$RT) # > length(RTs.norms.subjects$RT) # [1] 5440 # the number of observations in the no-errors database is: length(nomissing.full$RT) # so the number of errors is: length(RTs.norms.subjects$RT) - length(nomissing.full$RT) # > length(RTs.norms.subjects$RT) - length(nomissing.full$RT) # [1] 183 # is this enough to conduct an analysis of response accuracy? we can have a look but first we will need to create # an accuracy coding variable i.e. where error = 0 and correct = 1 RTs.norms.subjects$accuracy <- as.integer(ifelse(RTs.norms.subjects$RT > 0, "1", "0")) # we can create the accuracy variable, and run the glmm but, as we will see, we will get an error message, false # convergence likely due to the low number of errors
Notice:
— I am copying the outputs from function calls from the console window, where they appear, into the script file, where they are now saved for later reference.
— I find this to be a handy way to keep track of results, as I move through a series of analyses. This is because I often do analyses a number of times, maybe having made changes in the composition of the dataframe or in how I transformed variables, and I need to keep track of what happens after each stage or each operation.
— You can see that there were a very small number of errors recorded in the experiment, less than 200 errors out of 5000+ trials. This is a not unusual error rate, I think, for a dataset collected with typically developing adult readers.
In this post, I will add something new, using the ifelse() control structure to create an accuracy variable which is added to the dataframe:
# so the number of errors is: length(RTs.norms.subjects$RT) - length(nomissing.full$RT) # > length(RTs.norms.subjects$RT) - length(nomissing.full$RT) # [1] 183 # is this enough to conduct an analysis of response accuracy? we can have a look but first we will need to create # an accuracy coding variable i.e. where error = 0 and correct = 1 RTs.norms.subjects$accuracy <- as.integer(ifelse(RTs.norms.subjects$RT > 0, "1", "0")) # we can create the accuracy variable, and run the glmm but, as we will see, we will get an error message, false # convergence likely due to the low number of errors
Notice:
— I am starting to use the script file not just to hold lines of code to perform the analysis, not just to hold the results of analyses that I might redo, but also to comment on what I am seeing as I work.
— The ifelse() function is pretty handy, and I have started using it more and more.
— Here, I can break down what is happening step by step:-
1. RTs.norms.subjects$accuracy <- — creates a vector that gets added to the existing dataframe columns, that vector has elements corresponding to the results of a test on each observation in the RT column, a test applied using the ifelse() function, a test that results in a new vector with elements in the correct order for each observation.
2. as.integer() — wraps the ifelse() function in a function call that renders the output of ifelse() as a numeric integer vector; you will remember from a previous post how one can use is.[datatype]() and as.[datatype]() function calls to test or coerce, respectively, the datatype of a vector.
3. ifelse(RTs.norms.subjects$RT > 0, “1”, “0”) — uses the ifelse() function to perform a test on the RT vector such that if it is true that the RT value is greater than 0 then a 1 is returned, if it is not then a 0 is returned, these 1s and 0s encode accuracy and fill up the new vector being created, one element at a time, in an order corresponding to the order in which the RTs are listed.
I used to write notes on my analyses on paper, then in a word document (using CTRL-F that will be more searchable), to ensure I had a record of what I did.
It is worth keeping good notes on what you do because you (I) rarely get an unbroken interval of time in which to complete an analysis up to the report stage, thus you will often return to an analysis after a break of days to months, and you will therefore need to write notes that your future self will read so that analyses are self-explanatory or self-explained.
Check predictor collinearity
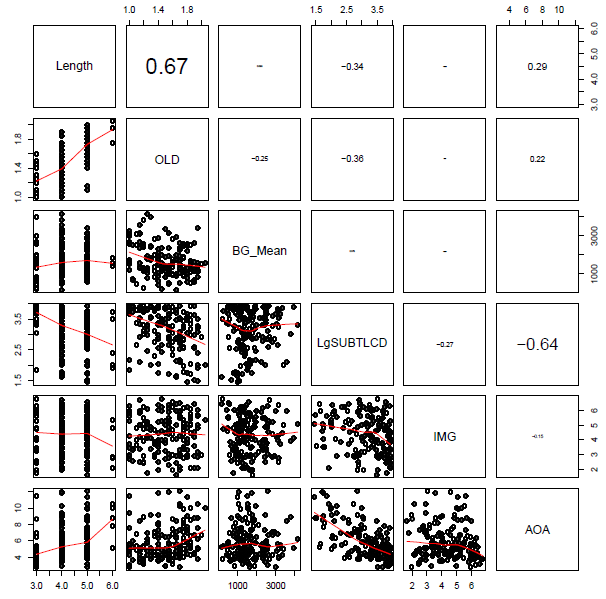
The next thing we want to do is to examine the extent to which our predictors cluster, representing overlapping information, and presenting potential problems for our analysis. We can do this stage of our analysis by examining scatterplot matrices and calculating the condition number for our predictors. Note that I am going to be fairly lax here, by deciding in advance that I will use some predictors but not others in the analysis to come. (If I were being strict, I would have to find and explain theory-led and data-led reasons for including the predictors that I do include.)
# check collinearity and check data distributions #########################################################
# we can consider the way in which potential predictor variables cluster together
summary(nomissing.full)
# create a subset of the dataframe holding just the potential numeric predictors
# NB I am not bothering, here, to include all variables, e.g. multiple measures of the same dimension
nomissing.full.pairs <- subset(nomissing.full, select = c(
"Length", "OLD", "BG_Mean", "LgSUBTLCD", "brookesIMG", "AoA_Kup_lem", "Age",
"TOWRE_wordacc", "TOWRE_nonwordacc", "ART_HRminusFR"
))
# rename those variables that need it for improved legibility
nomissing.full.pairs <- rename(nomissing.full.pairs, c(
brookesIMG = "IMG", AoA_Kup_lem = "AOA",
TOWRE_wordacc = "TOWREW", TOWRE_nonwordacc = "TOWRENW", ART_HRminusFR = "ART"
))
# subset the predictors again by items and person level attributes to make the plotting more sensible
nomissing.full.pairs.items <- subset(nomissing.full.pairs, select = c(
"Length", "OLD", "BG_Mean", "LgSUBTLCD", "IMG", "AOA"
))
nomissing.full.pairs.subjects <- subset(nomissing.full.pairs, select = c(
"Age", "TOWREW", "TOWRENW", "ART"
))
# draw a pairs scatterplot matrix
pdf("ML-nomissing-full-pairs-items-splom-110513.pdf", width = 8, height = 8)
pairs(nomissing.full.pairs.items, lower.panel=panel.smooth, upper.panel=panel.cor)
dev.off()
# draw a pairs scatterplot matrix
pdf("ML-nomissing-full-pairs-subjects-splom-110513.pdf", width = 8, height = 8)
pairs(nomissing.full.pairs.subjects, lower.panel=panel.smooth, upper.panel=panel.cor)
dev.off()
# assess collinearity using the condition number, kappa, metric
collin.fnc(nomissing.full.pairs.items)$cnumber
collin.fnc(nomissing.full.pairs.subjects)$cnumber
# > collin.fnc(nomissing.full.pairs.items)$cnumber
# [1] 46.0404
# > collin.fnc(nomissing.full.pairs.subjects)$cnumber
# [1] 36.69636
You will see when you run this code that the set of subject attribute predictors (see below) …
… and the set of item attribute predictors (see below) …
… include some quite strongly overlapping variables, distinguished by high correlation coefficients.
I was advised, when I started doing regression analyses, that a rule-of-thumb one can happily use when examining bivariate i.e. pairwise correlations between predictor variables is that there is no multicollinearity to worry about if there are no coefficients greater than however, I can think of no statistical reason for this number, while Baayen (2008) recommends using the condition number, kappa, as a diagnostic measure, based on Belsley et al.’s (1980) arguments that pairwise correlations do not reveal the real, underlying, structure of latent factors (i.e. principal components of which collinear variables are transformations or expressions).
If we calculate the condition number for, separately, the subject predictors and the item predictors, we get values of 30+ in each case. Baayen (2008) comments that (if memory serves) a condition number higher than 12 indicates a dangerous level of multicollinearity. However, Cohen et al. (2003) comment that while 12 or so might be a risky kappa there are no strong statistical reasons for setting the thresholds for a ‘good’ or a ‘bad’ condition number; one cannot apply the test thoughtlessly. That said, 30+ does not look good.
The condition number is based around Principal Components Analysis (PCA) and I think it is worth considering the outcome of such an analysis over predictor variables when examining the multicollinearity of those variables. PCA will often show that set of several item attribute predictors will often relate quite strongly to a set of maybe four orthogonal components: something to do with frequency/experience; something relating to age or meaning; something relating to word length and orthographic similarity; and maybe some thing relating to sublexical unit frequency. However, as noted previously, Cohen et al. (2003) provide good arguments for being cautious about performing a principal components regression in response to a state of high collinearity among your predictors, including problems relating to the interpretability of findings.
Center variables on their means
One perhaps partial means to alleviate the collinearity indicated may be to center predictor variables on their means.
(Should you center variables on their means before or after you remove errors, i.e. means calculated for the full or the no-errors dataframe? Should you center both predictors and the outcome variables? I will need to come back to those questions.)
Centering variables is helpful, also, for the interpretation of effects where 0 on the raw variables is not meaningful e.g. noone has an age of 0 years, no word has a length of 0 letters. With centered variables, if there is an effect then one can say that for unit increase in the predictor variable (where 0 for the variable is now equal to the mean for the sample, because of centering), there is a change in the outcome, on average, equal to the coefficient estimated for the effect.
Centering variables is helpful, especially, when we are dealing with interactions. Cohen et al. (2003) note that the collinearity between predictors and interaction terms is reduced (this is reduction of nonessential collinearity, due to scaling) if predictors are centered. Note that interactions are represented by the multiplicative product of their component variables. You will often see an interaction represented as “age x word length effects”, the “x” reflects the fact that for the interaction of age by length effects the interaction term is entered in the analysis as the product of the age and length variables. In addition, centering again helps with the interpretation of effects because if an interaction is significant then one must interpret the effect of one variable in the interaction while taking into account the other variable (or variables) involved in the interaction (Cohen et al., 2003; see, also, Gelman & Hill, 2007). As that is the case, if we center our variables and the interaction as well as the main effects are significant, say, in our example, the age, length and age x length effects, then we might look at the age effect and interpret it by reporting that for unit change in age the effect is equal to the coefficient while the effect of length is held constant (i.e. at 0, its mean).
As you would expect, you can center variables in R very easily, we will use one method, which is to employ the scale() function, specifying that we want variables to be centered on their means, and that we want the results of that operation to be added to the dataframe as centered variables. Note that by centering on their means, I mean we take the mean for a variable and subtract it from each value observed for that variable. We could center variables by standardizing them, where we both subtract the mean and divide the variable by its standard deviation (see Gelman & Hill’s 2007, recommendations) but we will look at that another time.
So, I center variables on their means, creating new predictor variables that get added to the dataframe with the following code:
# we might center the variables - looking ahead to the use of interaction terms - as the centering will # both reduce nonessential collinearity due to scaling (Cohen et al., 2003) and help in the interpretation # of effects (Cohen et al., 2003; Gelman & Hill, 2007 p .55) ie if an interaction is sig one term will be # interpreted in terms of the difference due to unit change in the corresponding variable while the other is 0 nomissing.full$cLength <- scale(nomissing.full$Length, center = TRUE, scale = FALSE) nomissing.full$cBG_Mean <- scale(nomissing.full$BG_Mean, center = TRUE, scale = FALSE) nomissing.full$cOLD <- scale(nomissing.full$OLD, center = TRUE, scale = FALSE) nomissing.full$cIMG <- scale(nomissing.full$brookesIMG, center = TRUE, scale = FALSE) nomissing.full$cAOA <- scale(nomissing.full$AoA_Kup_lem, center = TRUE, scale = FALSE) nomissing.full$cLgSUBTLCD <- scale(nomissing.full$LgSUBTLCD, center = TRUE, scale = FALSE) nomissing.full$cAge <- scale(nomissing.full$Age, center = TRUE, scale = FALSE) nomissing.full$cTOWREW <- scale(nomissing.full$TOWRE_wordacc, center = TRUE, scale = FALSE) nomissing.full$cTOWRENW <- scale(nomissing.full$TOWRE_nonwordacc, center = TRUE, scale = FALSE) nomissing.full$cART <- scale(nomissing.full$ART_HRminusFR, center = TRUE, scale = FALSE) # subset the predictors again by items and person level attributes to make the plotting more sensible nomissing.full.c.items <- subset(nomissing.full, select = c( "cLength", "cOLD", "cBG_Mean", "cLgSUBTLCD", "cIMG", "cAOA" )) nomissing.full.c.subjects <- subset(nomissing.full, select = c( "cAge", "cTOWREW", "cTOWRENW", "cART" )) # assess collinearity using the condition number, kappa, metric collin.fnc(nomissing.full.c.items)$cnumber collin.fnc(nomissing.full.c.subjects)$cnumber # > collin.fnc(nomissing.full.c.items)$cnumber # [1] 3.180112 # > collin.fnc(nomissing.full.c.subjects)$cnumber # [1] 2.933563
Notice:
— I check the condition numbers for the predictors after centering and it appears that they are significantly reduced.
— I am not sure that that reduction can possibly be the end of the collinearity issue, but I shall take that result and run with it, for now.
— I also think that it would be appropriate to examine collinearity with both the centered variables and the interactions involving those predictors but that, too, can be left for another time.
Run the models
What I will do next is perform three sets of mixed-effects model analyses. I will talk about the first set in this post.
In this first set, I shall compare models varying in the predictor variables included in the model specification. We shall say that models with more predictors are more complex than models with fewer predictors (a subset of the predictors specified for the more complex models).
I shall then compare models of differing in complexity to see if increased complexity is justified by improved fit to data.
This is in response to: 1. reading Baayen (2008) and Pinheiro & Bates (2000) 2. recommendations by a reviewer; though I note that the reviewer recommendations are, in their application, qualified in my mind by some cautionary comments made by Pinheiro & Bates (2000), and confess that any problems of application or understanding are surely expressions of my misunderstanding.
What I am concerned about is the level of complexity that can be justified in the ultimate model by the contribution to improved fit by the model of the observed data. Of course, I have collected a set of predictors guided by theory, custom and practice in my field. But, as you have seen, I might choose to draw on a large set of potential predictors. I know that one cannot – to take one option used widely by psycholinguistics researchers – simply inspect a correlation table, comparing predictors with the outcome variable, and exclude those predictors that do not correlate with the outcome. Harrell (2001) comments that that approach has a biasing effect on the likelihood of detecting an effect that is really there (consuming, ‘ghost degrees of freedom’, or something like that). So what should we do or how should we satisfy ourselves that we should or should not include one or more predictor variables in our models?
You could start complex and step backwards to the simplest model that appears justified by model fit to observed data. I will return to that option another time.
In this post, I will start with the simplest model and build complexity up. Simpler models can be said to be nested in more complex models, e.g. a simple model including just main effects vs. a more complex model also including interactions. I will add complexity by adding sets of predictors, and I will compare each proximate pair of simple model and more complex model using the Likelihood Ratio Test (Pinheiro & Bates, 2000; see, especially, chapter 2, pp. 75-).
We can compare models with the same random effects (e.g. of subjects or items) but varying in complexity with respect to the fixed effects, i.e. replicable or manipulated variables like item length or participant age, and, separately, models with the same fixed effects but varying random effects.
Note that in comparing models varying in random effects, one estimates those effects using restricted maximum likelihood: you will see the argument REML = TRUE in the lmer() function call, that is what REML means. Note that in comparing models varying in fixed effects one must estimate those effects using maximum likelihood: you will see the argument REML = FALSE in the lmer() function call, that is what FALSE means. See comments in Baayen (2008) and Pinheiro & Bates (2000); I will come back to those important terms to focus on understanding, another time, focusing in this post on just writing the code for running the models.
We can compare the more and less complex models using the Likelihood Ration Test (LRT) which is executed with the anova([simple model], [more complex model]) function call. A statistic is computed, and evaluated against the
distribution to estimate the probability of an increase in model likelihood as large or larger as that observed when comparing the more or less complex model, given the null hypothesis of no gain in likelihood.
Note that I log transform the RTs but one might also consider examining the reciprocal RT.
# we can move to some multilevel modelling ############################################################### # we might start by examining the effects of predictors in a series of additions of sets of predictors # we can hold the random effects, of subjects and items, constant, while varying the fixed effects # we can compare the relative fit of models to data using the anova() likelihood ratio test # in this series of models, we will use ML fitting full.lmer0 <- lmer(log(RT) ~ # Trial.order + # # cAge + cTOWREW + cTOWRENW + cART + # # cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer0,corr=F) # full.lmer1 <- lmer(log(RT) ~ Trial.order + # cAge + cTOWREW + cTOWRENW + cART + # # cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer1,corr=F) # full.lmer2 <- lmer(log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + # cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer2,corr=F) # full.lmer3 <- lmer(log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer3,corr=F) # full.lmer4 <- lmer(log(RT) ~ Trial.order + (cAge + cTOWREW + cTOWRENW + cART)* (cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG) + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer4,corr=F) # compare models of varying complexity anova(full.lmer0, full.lmer1) anova(full.lmer1, full.lmer2) anova(full.lmer2, full.lmer3) anova(full.lmer3, full.lmer4)
This code will first print out the summaries of each model, along the lines you have already seen. It will then give you this:
# > # compare models of varying complexity # > # > anova(full.lmer0, full.lmer1) # Data: nomissing.full # Models: # full.lmer0: log(RT) ~ (1 | subjectID) + (1 | item_name) # full.lmer1: log(RT) ~ Trial.order + (1 | subjectID) + (1 | item_name) # Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) # full.lmer0 4 -977.58 -951.31 492.79 # full.lmer1 5 -975.83 -943.00 492.92 0.2545 1 0.6139 # > anova(full.lmer1, full.lmer2) # Data: nomissing.full # Models: # full.lmer1: log(RT) ~ Trial.order + (1 | subjectID) + (1 | item_name) # full.lmer2: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + (1 | # full.lmer2: subjectID) + (1 | item_name) # Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) # full.lmer1 5 -975.83 -943.00 492.92 # full.lmer2 9 -977.09 -917.98 497.54 9.2541 4 0.05505 . # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # > anova(full.lmer2, full.lmer3) # Data: nomissing.full # Models: # full.lmer2: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + (1 | # full.lmer2: subjectID) + (1 | item_name) # full.lmer3: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + cLength + # full.lmer3: cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1 | subjectID) + # full.lmer3: (1 | item_name) # Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) # full.lmer2 9 -977.09 -917.98 497.54 # full.lmer3 15 -1115.42 -1016.91 572.71 150.34 6 < 2.2e-16 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # > anova(full.lmer3, full.lmer4) # Data: nomissing.full # Models: # full.lmer3: log(RT) ~ Trial.order + cAge + cTOWREW + cTOWRENW + cART + cLength + # full.lmer3: cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG + (1 | subjectID) + # full.lmer3: (1 | item_name) # full.lmer4: log(RT) ~ Trial.order + (cAge + cTOWREW + cTOWRENW + cART) * # full.lmer4: (cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG) + # full.lmer4: (1 | subjectID) + (1 | item_name) # Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) # full.lmer3 15 -1115.4 -1016.91 572.71 # full.lmer4 39 -1125.7 -869.56 601.84 58.262 24 0.0001119 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # it looks like the full model, including interactions but not the trialorder variable, is justified
Notice:
— It is not very pretty but it does tell you what predictors are included in each model you are comparing, for each pair of models being compared, the outcome of the ratio test, giving the numbers I usually report: the and the
.
— I am looking at this output to see if, for each pair of models, the more complex model fits the data significantly better (if p =< 0.05).
–I add predictors in blocks and assess the improvement of fit associated with the whole block.
I have made a lot of promises to explain things more another time. So I will add one more. Pinheiro & Bates (2000; p. 88) argue that Likelihood Ratio Test comparisons of models varying in fixed effects tend to be anticonservative i.e. will see you observe significant differences in model fit more often than you should. I think they are talking, especially, about situations in which the number of model parameter differences (differences between the complex model and the nested simpler model) is large relative to the number of observations. This is not really a worry for this dataset, but I will come back to the substance of this view, and alternatives to the approach taken here.
Get the p-values
Finally, we request the generation of p-values for the effects we have entered in the model with the most justifiable complexity.
# get p-values full.lmer4 <- lmer(log(RT) ~ Trial.order + (cAge + cTOWREW + cTOWRENW + cART)* (cLength + cOLD + cBG_Mean + cLgSUBTLCD + cAOA + cIMG) + (1|subjectID) + (1|item_name), data = nomissing.full, REML = FALSE) print(full.lmer4,corr=F) pvals.fnc(full.lmer4)$fixed
and the combination of the last commands, to print a summary of the model, and to calculate p-values, will tell you that:-
— We have significant effects due to:
cAge + cART + cTOWRENW +
cLength + cOLD + cBG_Mean + cLgSUBTLCD + cIMG +
cTOWRENW:cLgSUBTLCD + cAge:cLength + cAge:cOLD + cAge:cBG_Mean
I am writing the interactions not as var1*var2 but as var1:var2 – the second form of expressing an interaction restricts the analysis to considering just that product term whereas the first requires the analysis to consider the products and all its components. We must, if include an interaction in our model also include all its main effects components – try not doing this, you should get an error – however, I have found that if you were to include e.g. age*length and also age*OLD there are problems while the more restrictive age:length and age:OLD seems to deal with that problem. I have a feeling Baayen (2008) explains this better but I do not have a copy to hand and therefore cannot relay his explanation here.
— The initial summary of the model shows fixed and random effects estimates but does not give you p-values. Baayen et al. (2008) explain that if we were doing ordinary least squares regression, the method for calculating p-values has been well worked out, assuming just the fixed effects plus a single parameter corresponding to random (normally distributed) error, with a calculation of model degrees of freedom corresponding to estimated effects and residual degrees of freedom corresponding to the number of observations less the number of effects. It is hard to calculate degrees of freedom for mixed-effects models: should we count the number of subjects, or of items, or, somehow, both?
— Baayen et al. (2008) argue that what we want is to understand the imprecision of our estimate of the random errors when looking at our fixed effects. This is what we can achieve with Markov chain Monte Carlo simulations, the source of the p-values we report.
— The t- and MCMC-derived p-values will tend to coincide for most analyses.
— We get significant effects that appear to make sense: effects of age, reading experience, length (though longer words elicit shorter RTs), frequency, AoA (near significant), imageability, and interactions between age and length, age and Orthographic Levenshtein Distance (OLD), age and mean bigram frequency, nonword reading skill and frequency.
What next?
What I would seek to do in the next series of analyses is determine if the effects that are significant appear to be significant due:
1. to the presence of other, nonsignificant effects — making the check by removing the nonsignificant effects then rerunning the model;
2. to the presence of outlier observations — making the check by removing observations associated with large model residuals then rerunning the model.
What have we learnt?
(The code I have used in running the analysis described in this post can be found here.)
Firstly, I am going to have to do a lot more explaining, for my own sake, and have promised to do so for a wide range of ideas, including those concerning the methods of model fitting, and, especially, the discussion around how one determines the appropriate set of fixed effects.
Secondly, that the model code is both simple and – on its face – reasonably intuitive.
Key vocabulary (mostly, a list of things to be explained)
fixed effects
random effects
random intercepts
random slopes
interactions
multiplicative products
centering
maximum likelihood
restricted maximum likelihood
Markov chain Monte Carlo
Likelihood Ratio Test
lmer()
anova()
pvals.fnc()
Reading
Baayen, R. H. (2008). Analyzing linguistic data. Cambridge University Press.
Bates, D. M. (2005). Fitting linear mixed models in R. R News, 5, 27-30.
Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. New York: Wiley.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioural sciences (3rd. edition). Mahwah, NJ: Lawrence Erlbaum Associates.
Gelman, A., & Hill, J. (2007). Data analysis using regression and multilevel/hierarchical models. New York,NY: Cambridge University Press.
Pinheiro, J. C., & Bates, D. M. (2000). Mixed-effects models in S and S-plus (Statistics and Computing). New York: Springer.