Modelling – next steps

Posted on May 7, 2013 by robayedavies

Having dwelt on the relationships between pairs of variables, both in terms of scatterplot depictions and, lately, in terms of correlations, we can move on to the real core of our focus in analyzing psycholinguistic data: linear regression.

cuba-yellow-CC-Florida-Memory

Creative commons – flickr – State Library and Archives of Florida – Florida Memory: Street vendor and patrons, Havana Cuba, 1950

— This image just caught my eye because of the yellows.

The next posts will build through:

1. A consideration of linear regression ideas;

2. Linear regression steps in R;

3. The groundwork for an extension of regression to mixed-effects modelling;

4. Mixed-effects modelling in R.

I will return to some steps repeatedly over time.

Posted in .Interim directions, modelling, rstats | Tagged , | Leave a comment

Getting started – revision of dataframe input, new on looking at data type

Posted on May 5, 2013 by robayedavies

This post assumes that you have read and worked through examples in previous posts concerning: 1. how to read in .csv files as dataframes; 2. data structure basics, including discussion of vectors, matrices, and dataframes. We will be working with the items data previously referenced here.

frame-CC-US-National-Archives

flickr – Creative Commons – US National Archives: Rising the first main frame of a dirigible, ca. 1933

Here we will look at dataframes in more detail because dataframes will be, generally, what we will be dealing with in our data analyses. We will revise how you can input a database from an external source, e.g. an excel .csv file, and read it into the R workspace as a dataframe. We will also look at how you can test and convert the data type of variables in a dataframe.

In the next post, we will look at how you refer to elements of a dataframe by place, name or condition, and how you use that capacity to add to or remove from the dataframe and how you subset dataframes.

Revision: downloading external databases

If you recall my post on workflow, in the research I do and supervise, we typically work through a series of stages that end in a number of data files: select items and prepare a script to present those items (as stimuli) and collect responses (usually reading responses); we test people and collect data; we collate the data, often with some cleaning; we do analyses in R. The data collation phase will typically yield a number of data files, and I usually create such files in excel (where collation and cleaning is done  by hand), outputting them as .csv files.

It is straightforward getting the data files into R, provided you have set your working directory correctly.

I am going to assume that you have managed to download the item norms data files from the links give at this post, or in the following reiteration of the main text:

We have .csv files holding:

1. data on the words and nonwords, variables common to both like word length;

2. data on word and nonword item coding, corresponding to item in program information, that will allow us to link these norms data to data collected during the lexical decision task;

3. data on just the words, e.g. age-of-acquisition, which obviously do not obtain for the nonwords.

Notice:

— We have data on the characteristics of 160 words and 160 nonwords, selected using the English Lexicon Project nonwords interface which is really very useful.

— The words are supposed to be matched to the nonwords on length and other orthographic characteristics to ensure that participants are required to access the lexicon to distinguish the real words from the made-up words (the nonwords). We can and will test this matching using t-tests (in another post).

Revision: getting external databases into R using read()

We can set the working directory and input the databases in a few lines of code:


# set the working directory

setwd("C:/Users/p0075152/Dropbox/resources R public")

# read in the item norms data

item.norms <- read.csv(file="item norms 270312 050513.csv", head=TRUE,sep=",", na.strings = "-999")
word.norms <- read.csv(file="word norms 140812.csv", head=TRUE,sep=",", na.strings = "-999")
item.coding <- read.csv(file="item coding info 270312.csv", head=TRUE,sep=",", na.strings = "-999")

Notice:

— The code here specifies that we are reading in or inputting comma delimited files, .csv, using the read.csv() function call.

— We specified that we wanted the column names for the variables with head= TRUE.

— We also specified that the values in different columns in the dataframe were delimited by commas — check what happens if this bit of the code is taken out.

— Finally, we specified that missing values in the database – referred to in R as NA or not available – should be recognized wherever there is a value of -999; I use -999 to code for missing values when I am building databases, you might choose something different.

— N.B. We might equally have used read.table(): a more general form of the read function.

Revision: getting information about dataframe objects

We have looked at how to get information about dataframes before. There are a number of very useful function, and you can enter the following code to get information about the various databases you have just put into the workspace.


# get summary statistics for the item norms

head(item.norms, n = 2)
summary(item.norms)
describe(item.norms)
str(item.norms)
length(item.norms)
length(item.norms$item_name)

If you run that code on the item.norms dataframe, you will see something like this in the console window (below the script window):

R-4-10-df-descriptives

Notice:

— head() will give you the top rows from the data frame, the n = argument in head(item.norms, n = 2) is a specification that we want the top 2 rows but you could ask for any number, try it.

— summary() will give you information about factors like item_type, telling you how many times each level in the factor occurs, as well as statistical data about numeric variables like (in this dataframe) Length, including median and mean.

— describe() will give you the mean, SD and other statistics often required for report

— str() is very useful because it indicates what data mode or type each variable is identified to have by R.

— length() will tell you how many variables there are in the dataframe.

— length(item.norms$item_name) tells us how many observations or elements there are in the variable or vector item.norms$item_name.

$ – Referring to dataframe variables by name

Notice the use of the item.norms$item_name notation.

What we are doing here is referring to a specific variable in a dataframe by name using the notation: dataframe’s-name-$-vector-name.

Note that you can avoid having to write dataframe$variable and just refer to the variable if you use the attach() function, however, some people regard that as problematic (consider if more than one variable exists with the same name) and so I will not be using attach().

Using descriptive information about dataframes to examine their state

I would use one or more of the summary functions to examine whether the dataframe I have input is in the shape I expect it to be.

I usually inspect dataframes as I input them, at the start of an analysis. I am looking for answers to the following questions:-

1. Does the dataframe have the dimensions I expect? I have usually built the dataset in excel by hand so I have a clear idea about the columns (variables) that should be in it, their names, and the number of rows (observations). Even for a dataset with several thousand observations, I should still be able to tell precisely how many should be in the dataframe resulting from the read() function call.

2. Are the variables of the datatype I expect? Using the str() and summary() function calls, I can tell if R regards variables in the same way as I do.

In an earlier version of this post, I noted that the item.norms dataframe inspection yielded a surprise:

— I expected to see the bigram frequency variables, BG_Sum, BG_Mean, BG_FreqBy_Pos, to all be treated as numeric variables, but saw in the output from the str() function call, that R thought they were factors. I think this happened because the ELP yields BG numbers with “,” as a delimiter for numbers in the 1,000s. The presence of the “,” triggered the recognition by R of these variables as factors. I fixed that in excel by reformatting the cells, removing the “,” but one could use the functions discussed at the end.

3. Are the missing values in the dataset, and have they been coded correctly? Needs will vary between analyses. As, typically, analyses of the data yielded by psycholinguistic experiments often are analyses of the latency of correct responses, we will need to exclude errors before analysis, which we could do by first coding them as missing values (-999 in the database when it is built, -999 assigned as NA in R when input), then omitting the NAs.

I don’t think it ever pays to omit a careful movement through this phase because any errors that go undetected here will only waste your time later.

Data modes, testing for mode, and changing it

As mentioned previously, data objects in R have structure (e.g. a vector or a dataframe etc.) and mode: R can deal with numeric, character, logical and other modes of data.

Usually, if you think a variable is numeric, character etc., R will think so too.

Let’s consider the different data types before we consider how to test a variable for type and then how to convert variable types (coercion). See this helpful post in the Quick-R blog, or chapter 2 in R-in-Action (Kabacoff, 2011) for further information.

Data types

— factor: categorical or nominal data, with a small number of distinct values (levels) e.g. the factor gender with levels male and female, or the factor item type with levels word and nonword, or the factor subject with levels one for each different person in a dataset; factors can be ordered or unordered (ordinal data).

— numeric: numbers data, could be of types double precision or integer [will need to look these things up but think not relevant yet as referring to more sophisticated distinctions]

— character: data consisting of characters, could be intended as numbers or factors

[This is a bit weak but will do for now.]

— dealing with dates and times is a whole other world of stuff to take on, and we will come to that stuff later

Testing variables for mode

There are some very useful functions in R for testing the mode of a variable.

Let’s start by checking out the BG_ variables.


# if we inspect the results of the input, we can check the assignment of data mode to the vectors
# in our data frames

is.factor(item.norms$BG_Sum)
is.factor(item.norms$BG_Mean)
is.factor(item.norms$BG_Freq_By_Pos)

is.numeric(item.norms$BG_Sum)
is.numeric(item.norms$BG_Mean)
is.numeric(item.norms$BG_Freq_By_Pos)

You will see that if you run these lines of code:

1. R will return the result FALSE to the test is.factor() because the BG bigram frequency variables are classed as of type numeric;

2. R will return TRUE for is.numeric() because the bigram variables are not of type factor.

Converting (coercing) variable types – coercing data vector mode

There are some very useful functions in R for converting or coercing a variable’s mode from one kind to another, if required.

We can convert a variable’s data type using the as.factor(), as.numeric() functions; there is also as.character().

For example, we can convert BG_Sum from a numeric variable to a factor and back again using as.factor() and as.numeric(). With each conversion, we can demonstrate the variable’s data type by testing it using is.factor() or is.numeric() and also by getting str() and summary() results for the variable.


# convert the BG_Sum variable from being numeric to being a factor:

item.norms$BG_Sum <- as.factor(item.norms$BG_Sum)

# check the variable type

is.factor(item.norms$BG_Sum)
is.numeric(item.norms$BG_Sum)

# show structure and summary

str(item.norms$BG_Sum)
summary(item.norms$BG_Sum)

# convert the variable back from factor to numeric

item.norms$BG_Sum <- as.numeric(item.norms$BG_Sum)

# check the variable type

is.factor(item.norms$BG_Sum)
is.numeric(item.norms$BG_Sum)

# show structure and summary

str(item.norms$BG_Sum)
summary(item.norms$BG_Sum)

Try this out for yourself, inspecting the result of each conversion.

Notice:

— I am doing the conversion using the as.factor() or as.numeric() function calls.

— I am asking that the converted variable is given the same name as the original type variable. I could ask for the converted variable to be given a new name e.g. item.norms$newBG_Sum.

What have we learnt?

[The code used in this post can be downloaded from here.]

We have revised how you input a dataframe, getting it from a file in your computer folder to an object in the workspace.

We have revised how you get information to inspect the dataframe.

We have looked at how you test, and how you can convert, the type of data a variable is treated as.

Key vocabulary

read.csv()

summary()

head()

describe()

str()

is.numeric()

is.factor()

as.numeric()

as.factor()

Posted in 8. Getting started - data, getting started, rstats | Tagged , , , , , , | Leave a comment

Modelling – examining correlations among predictors

Posted on May 5, 2013 by robayedavies

In a previous post, we used merge() to create a joint database holding a large set of data on the attributes of the 160 words presented in a lexical decision experiment whose completion I supervised a while ago.

I would like to use these variables to examine the reading behaviour – here, visual word recognition measured in lexical decision – of the participant sample examined in a series of previous posts (starting here).

As noted here and here, a concern over the use of word attribute variables is that everything seems to correlate with everything else, which could cause problems for our analyses. So what I would like to do is begin by examining the correlations among the item attribute variables that are available to me.

It might be worth looking at the slides I prepared earlier on correlations, here:

https://speakerdeck.com/robayedavies/r-class-correlations

— the materials in these slides are based on Howell (2002) and Cohen, Cohen, Aiken and West (2003), in particular.

We have seen, previously, how to examine the way in which one particular variable might be related or relate to a set of other variables, when we looked at the subjects data here, and when we previously looked at the items data here.

I won’t repeat that exercise because when we are looking at item attributes we typically wish to know how everything relates to everything else, due to our concern with collinearity.

See Baayen et al. (2006) for an interesting, and illuminating, analysis of the way in which the age-of-acquisition, imageability or subjective rated frequency of a word can be predicted by these and other lexical variables

At this point, what we want to do is simply examine the relationship of all variables with all other variables.

We will focus, here, on the set of 160 words that were presented to participants in ML’s lexical decision study.

Get the data

Having previously compiled the item word attributes data to a single new database (downloadable here) from the item.norms and word.norms dataframes, we can just load that to our workspace as follows:


# set the working directory

setwd("C:/Users/p0075152/Dropbox/resources R public")

# read in the item norms data

item.norms <- read.csv(file="item norms 270312 050513.csv", head=TRUE,sep=",", na.strings = "-999")
word.norms <- read.csv(file="word norms 140812.csv", head=TRUE,sep=",", na.strings = "-999")
item.coding <- read.csv(file="item coding info 270312.csv", head=TRUE,sep=",", na.strings = "-999")

# read in the merged new dataframe

item.words.norms <- read.csv(file="item.words.norms 050513.csv", head=TRUE,sep=",", na.strings = "NA")

Notice:

— In the read.csv() function call for inputting the item.words.norms dataframe, I switched the na.strings = argument to na.strings = “NA”.

— If I had not done this, R would treat the Cortese imageability and AOA variables as factors because those columns include both numbers and strings; the NA strings were written in the item.words.norms .csv output due to missing values on these attributes for some items. (These data were collected and made available by Cortese and colleagues, see, for reports on how the ratings were collected: Cortese & Fuggett, 2004; Cortese & Khanna, 2008) .

— The presence of “NA” character strings in the imageability or AOA columns ensures that these variables get treated as factors. You will recall that vectors are allowed to have data of one type only: R sees the NAs and classes the vectors as of type factor.

Visualizing the relationships between many variables simultaneously

What I would like to do next is to create what is called a scatterplot matrix, see here and here for some online resources. Winston Chang’s (2013) R Graphics Cookbook has nice tips also.

A scatterplot matrix is a useful way to visualize the relationships between all possible pairs of variables in a set of predictors. In my experience, it does not work very well for large (n > 5) sets of variables but has a nice impact when it does work well.

Define a scatterplot matrix function

I like the plots produced by a function shared by William Revelle here:

http://www.personality-project.org/r/r.graphics.html

You have to start by defining a function to draw the plot:


#code taken from part of a short guide to R
#Version of November 26, 2004
#William Revelle
# see: http://www.personality-project.org/r/r.graphics.html

panel.cor <- function(x, y, digits=2, prefix="", cex.cor)
{
 usr <- par("usr"); on.exit(par(usr))
 par(usr = c(0, 1, 0, 1))
 r = (cor(x, y))
 txt <- format(c(r, 0.123456789), digits=digits)[1]
 txt <- paste(prefix, txt, sep="")
 if(missing(cex.cor)) cex <- 0.8/strwidth(txt)
 text(0.5, 0.5, txt, cex = cex * abs(r))
}

Subset the variables for plotting

You then need to create a subset of the variables from your dataframe. You don’t want to include factors (at least for this plot), and we do not want to try to create a matrix with too many plots in it. We can use the knowledge about subsetting developed in a previous post to do the subsetting as follows.


norms.pairs <- subset(item.words.norms, select = c(

 "Length", "Ortho_N", "BG_Mean", "LgSUBTLCD", "brookesIMG", "AoA_Kup_lem"

 ))

Notice:

— Variable names are given in a vector c() call, with names in “”.

— I am separating out the lines on which the parts of the function call appear for, to me, improved readability: first line gives the main bits; second line gives the arguments; last line wraps it up with the matching parentheses.

Rename the variables for readability

I am going to need to have the names a bit more concise, to improve readability in the scatterplot matrix. So I will use the rename() function demonstrated previously.


norms.pairs.2 <- rename(norms.pairs, c(

 Ortho_N = "N", BG_Mean = "BGM", LgSUBTLCD = "logCD", brookesIMG = "IMG", AoA_Kup_lem = "AOA"

))

All of which will deliver a dataframe that we can feed into the scatterplot matrix function:

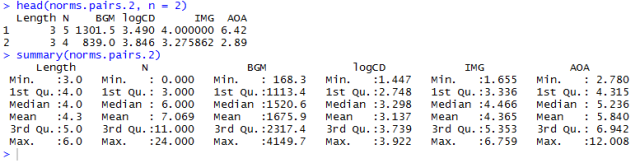
R-6-10-pairs

Notice:

— In renaming the pairs dataframe variables, I created a new dataframe and appended the .2 for me this is just good housekeeping: it helps to ensure I am not overwriting stuff I might want at a later time i.e. original versions of data.

Feed the pairs dataframe into the pairs plot or scatterplot matrix function

Now we can just run the function to get the scatterplot matrix as:


pdf("ML-item-norms-words-pairs-050513.pdf", width = 8, height = 8)

pairs(norms.pairs.2, lower.panel=panel.smooth, upper.panel=panel.cor)

dev.off()

which gives you this:

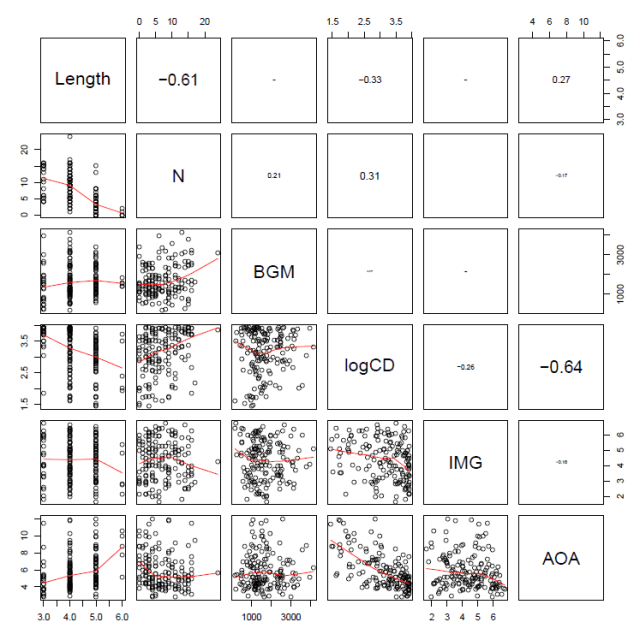
R-6-11-splom

Notice:

— The printout size of the correlation coefficient is scaled by its value.

— We can see the correlations between Length and neighbourhood (N) and between frequency (logCD) and age-of-acquisition (AOA) illustrated both in terms of the Pearson’s correlation coefficients, r, in the upper panels, and visually as a scatterplot with a LOESS smoother in the lower panels.

— Note the scatterplot corresponding to the correlation coefficient is the one opposite it in the grid.

Correlation table

Conventionally, while scatterplot matrices are nice (the combination of information is enlightening), reports in journals include tables of correlations.

Again, a kind R-user (named myowelt) provided the code I need to produce a table, and posted it here.

Note that you will need to have the Hmisc or rms packages installed, and the corresponding libraries loaded, to get this function to work.

You can copy and paste this into the R script window, then run the code to define the function we will use to then generate a table of correlation coefficients (Pearson’s r) with stars to indicate significance and everything.


corstarsl <- function(x){
 require(Hmisc)
 x <- as.matrix(x)
 R <- rcorr(x)$r
 p <- rcorr(x)$P

 ## define notions for significance levels; spacing is important.
 mystars <- ifelse(p < .001, "***", ifelse(p < .01, "** ", ifelse(p < .05, "* ", " ")))

 ## trunctuate the matrix that holds the correlations to two decimal
 R <- format(round(cbind(rep(-1.11, ncol(x)), R), 2))[,-1]

 ## build a new matrix that includes the correlations with their apropriate stars
 Rnew <- matrix(paste(R, mystars, sep=""), ncol=ncol(x))
 diag(Rnew) <- paste(diag(R), " ", sep="")
 rownames(Rnew) <- colnames(x)
 colnames(Rnew) <- paste(colnames(x), "", sep="")

 ## remove upper triangle
 Rnew <- as.matrix(Rnew)
 Rnew[upper.tri(Rnew, diag = TRUE)] <- ""
 Rnew <- as.data.frame(Rnew)

 ## remove last column and return the matrix (which is now a data frame)
 Rnew <- cbind(Rnew[1:length(Rnew)-1])
 return(Rnew)
}

Notice:

— myowelt points out that you can use the xtables package to generate latex tables for a latex report.

— He also points out that much of the code was adapted from a nabble thread (follow the link above to go to the source then).

Having defined the correlations table function, we just feed the normative dataframe into it to get the result we want:


corstarsl(norms.pairs.2)

which delivers this:

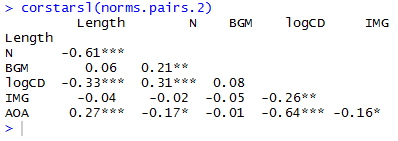
R-6-12-correlations

If you’re not writing in latex then you can paste this into a .txt file in notepad or something, open that in excel, format it for APA style, copy and paste the result into a word as a bitmap.

Cluster analysis diagrams

Correlation tables and scatterplot matrices are not the only way to examine the correlation structure of a set of variables.

In reading Baayen (2008; see, also, Baayen, Feldman, & Schreuder, 2006), I found that we can also examine a set of predictors in terms of clusters of variables.

Baayen (2008) notes that the Design package provides a function for visualizing clusters of variables, varclus(). I think that if you have rms package installed and the library loaded then that will bring the Design function package functions with it.

Paraphrasing Baayen (2008; p. 182-183): The varclus() function performs a hierarchical cluster analysis, using the square of Spearman’s rank correlation (a non-parametric correlation) as a similarity metric to obtain a more robust insight into the correlation structure of a set of variables.

We can run the function call very easily, as:


pdf("ML-item-norms-words-varclus-050513.pdf", width = 8, height = 8)

plot(varclus(as.matrix(norms.pairs.2)))

dev.off()

which gets you this:

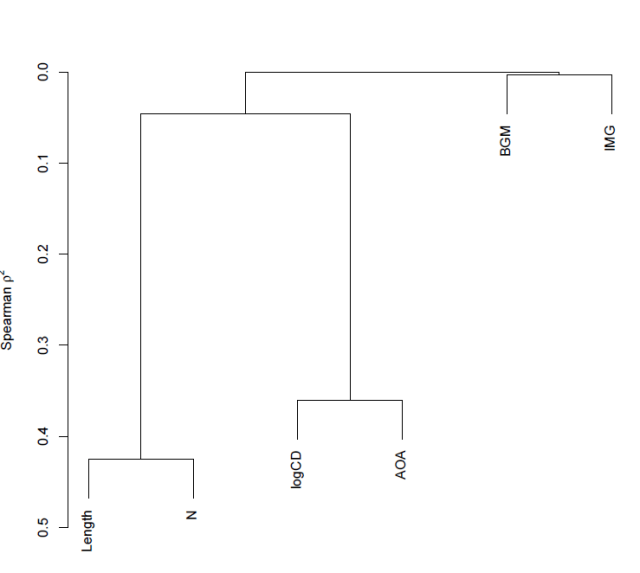
R-6-13-varclus

Notice:

— The y-axis corresponds to Spearman’s rho squared – the similarity measure.

— We know, given the foregoing, that length and neighbourhood are very similar to each but not very similar to anything else, likewise, logCD frequency and AoA are very similar to each other but not similar to anything else.

— Imageability and bigram frequency are not much related to anything.

— The diagram reflects these observations faithfully.

— The higher in the tree, the less similar you are – that is how I would interpret the relative placing of the splits i.e. the points at which the tree branches.

Note:

1. Hierarchical cluster analysis is a family of techniques for clustering data and displaying that clustering in a tree diagram.

2. These techniques take a distance object as input.

3. There are many different ways to form clusters.

I think that what we talking about here is: First, get a table of correlations. Use Spearman’s for robust estimation of correlations (robust to, say, the possibility that variables are not normally distributed). We can take the correlation between two variables as a measure of the distance between them i.e. similarity. As correlations can be negative or positive and we want distances to run in one direction only, we square the correlations. Convert the correlation matrix into a distance object (I am reading Baayen, 2008; p. 140, and I am not sure what that involves). One can then examine clustering by a number of different methods. One, divisive clustering, starts with all data points in a cluster then successively partitions clusters into smaller clusters. Another, agglomerative clustering, implemented in the hclust() function which, I think, is the basis for varclus(), begins with single data points which are then stuck together into successively larger groups.

What we are looking at, when we look at a tree diagram showing a clustering analysis, then, is  a set of variables split by their relative similarity.

This is definitely a placeholder for further research.

What I would like to find out is whether we can use techniques like this to sort participants into clusters according to their scores in the various measures of individual differences that we use.

Diagnosing when the correlation of variables is a problem – collinearity and the condition number

As noted previously, we are considering the relationships between variables because we are concerned with the problems associated with high levels of intercorrelation.

I would read both Baayen (2008) and Cohen, Cohen, Aiken, & West (2003) on multicollinearity (see also Belsley et al., 1980), for a start.

Cohen et al. (2003) describe a set of problems, grouped under the term multicollinearity, that arise from high levels of correlation between predictors. In regression analysis, we assume that each predictor can potentially add to the prediction of the outcome or dependent variable. As one of the predictors (or independent variables) becomes increasingly correlated with the other predictors, it will have increasingly less unique information that can contribute to the prediction of the outcome variable. This cause a variety of problems when the correlation of one predictor with the others becomes very high:

1. The regression coefficients – the estimates of effects of the variables – can change in direction and in size i.e. in sign and magnitude, making them difficult to interpret. We are talking, here, about inconsistency or instability of effects estimates between analyses (maybe with differing predictor sets) and studies, I think.

2. As predictors become increasingly correlated, the estimate of individual regression coefficients becomes increasingly unreliable. Small changes in the data, adding or deleting a few observations, can result in large changes in the results of regression analyses.

To understand the problem, look back at the scatterplots we have drawn and consider the relationships between the variables that we have shown. To take a (to me) classic example (see e.g. Zevin & Seidenberg, 2002), if we examine the effect of frequency or of AoA on reading behaviour, given the strong relationship between these variables, which is the variable that ‘truly’ is affecting reading? In terms of regression analysis, if you have both frequency and AoA as predictors, given their overlap, the shared information, how will you be able to distinguish the contribution of one or the other? What will it take for AoA or frequency or both to be observed to effect behaviour?

Cohen et al. (2003) note that in cross-sectional research, serious multicollinearity most commonly occurs when multiple measures of the same or similar constructs are used as the predictors in a regression; in my work, consider measures of word and nonword reading ability, or measures of word frequency and word AoA. In longitudinal research, serious multicollinearity often occurs when similar measures collected at previous time points are used to predict participant performance at some later time point.

If this makes you think that multicollinearity is going to be a problem for you all the time, I think that that would be correct – except where you can orthogonalize predictors through the manipulation of conditions.

How can we diagnose multicollinearity?

Again, repeating Cohen et al. (2003; pp. 419 -) [the following is mostly copied, with some paraphrase, and plenty of elision, as a placeholder for a thought-through explanation]:

The Variance Inflation Factor (VIF) provides an index of the amount that variance of each regression coefficient is increased compared to a situation in which all predictors are uncorrelated.

…

The condition number, kappa, is defined in terms of the decomposition of a correlation matrix into orthogonal i.e. uncorrelated components. The correlation matrix of predictors can be decomposed into a set of orthogonal dimensions (i.e. Principal Components Analysis). When this analysis is performed on the correlation matrix of k predictors, a set of  k eigenvalues or characteristic roots of the matrix is produced. The proportion of the variance in the predictors accounted for by each orthogonal dimension is lambda divided by k, where lambda is the eigenvalue. As the predictors become increasingly correlated, increasingly more of the variance in the predictors is associated with one dimension, and the value of the largest eigenvalue is correspondingly greater than the value of the smallest. At the maximum, all the variance in the predictors is accounted for by one dimension. The condition number is defined as the square root of the ratio of the largest eigenvalue compared to the smallest eigenvalue.

Baayen’s languageR package furnishes the collin.fnc() function for calculating the condition number for a set of predictors:


collin.fnc(norms.pairs.2)$cnumber

The result returned is 44.8 or so, which indicates a level of collinearity greater than that set as risky e.g. by Baayen (2008).

Cohen et al. (2003) comment that condition numbers greater than 30 are taken to reflect risky levels of multicollinearity but that there is no strong statistical rationale for such a threshold.

They advise that multicollinearity indices are no substitute for basic checks: outliers may affect multicollinearity; we should compare results of analyses with and without collinear predictors and examine changes in direction or size of observed effects; and we should take into account situations where multicollinearity may occur due to scaling – use of dummy coding variables – and therefore might not be so problematic.

It would be tempting to calculate the condition number, and address values of kappa through one or more remedies, but that, in sum, will not suffice.

Cohen et al. (2003) note that there are four potential solutions to multicollinearity, which we shall examine in later posts:

— We could combine variables e.g. through averaging across a set of predictors that all reflect some underlying construct.

— We could delete variables, though the choice for deletion will be worrisome.

— We could collect more data.

— Ridge regression where a constant is added to the variance of each predictor.

— Principal components regression, a method I have myself used (see e.g. Baayen et al., 2006; see Baayen, 2008, for a how-to guide), where Principal Components Analysis is used to derive a set of orthogonal i.e. uncorrelated dimensions or components from a set of collinear predictors. Cohen et al. (2003) note that these components are only rarely interpretable. Regression on principal components is limited to regression equations that are linear in the variables – no interactions or polynomial terms (Cohen et al., 2003, cite Cronbach, 1987) – though Baayen et al. (2006) report a regression involving principal components and including nonlinear terms.

I suspect, also, that Principal Components regression will work for some studies with large stimulus sets but will be biased for studies with smallish (n < 1000) stimulus sets.

I note, also, that Baayen et al. (2006) use Principal Components regression but also examine regressions where they use residualized predictors. Here, if you can predict one variable from the others (i.e. for a set of collinear predictors), you first perform a regression and get the residuals – that part of the predictor’s variance that is not predicted by the other predictors i.e. is orthogonal to them, you then use such residualized predictors in your analysis.

Do not imagine that your problems would be solved by splitting your items into selected item sets according to some factorial design, in which you get variation in one dimension e.g. frequency while controlling for variation in all other attributes. Balota et al. (2004) lay out very clearly how factorial (stimulus selection) designs in psycholinguistics experiments can be associated with a constellation of problems. Cohen (1983) explains very clearly the cost in loss of statistical sensitivity of dichotomizing continuous variables (if there’s an effect, you might be reducing your chances of observing it to something like a coin flip). Better, I think, to run a regression style study and take the multicollinearity on the chin: diagnose, check, treat, analyse, check.

Note, finally, that Cohen et al. (2003) distinguish essential from nonessential from essential multicollinearity (after Marquardt, 1980, cited in Cohen et al., 2003), a distinction relevant especially to analyses involving polynomial and interaction terms. Nonessential collinearity, due to scaling, can be removed through centering predictors, and we shall look at this again.

What have we learnt?

(The code for these analyses can be found here.)

We have learnt how to examine the correlations between all pairs among a set of variables.

Using the scatterplot matrix, the correlation table, and the variance clustering tree diagram to show the correlations.

Using the condition number to make a diagnosis of collinearity.

We have discussed what multicollinearity means, how to diagnose it, and some potential means to remedy it.

Key vocabulary

correlation

multicollinearity

clustering

Principal Components Analysis

regression

ridge regression

Principal Components regression

scatterplot matrix

condition number, kappa

varclus()

collin.fnc()

corstarsl()

Reading

Baayen, R. H. (2008). Analyzing linguistic data. Cambridge University Press.
Baayen, R. H., Feldman, L. B., & Schreuder, R. (2006). Morphological influences on the recognition of monosyllabic monomorphemic words. Journal of Memory and Language, 55, 290-313.
Balota, D., Cortese, M. J., Sergent-Marshall, S. D., Spieler, D., & Yap, M. (2004). Visual word recognition of single-syllable words. Journal of Experimental Psychology: General, 133, 283-316.
Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. New York: Wiley.
Chang, W. (2013). R Graphics Cookbook. Sebastopol, CA: o’Reilly Media.
Cohen, J. (1983). The cost of dichotomization. Applied Psychological Measurement, 7, 249-253.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioural sciences (3rd. edition). Mahwah, NJ: Lawrence Erlbaum Associates.
Cortese, M.J., & Fugett, A. (2004). Imageability Ratings for 3,000 Monosyllabic Words. Behavior Methods and Research, Instrumentation, & Computers, 36, 384-387.
Cortese, M.J., & Khanna, M.M. (2008). Age of Acquisition Ratings for 3,000 Monosyllabic Words. Behavior Research Methods, 40, 791-794.
Howell, D. C. (2002). Statistical methods for psychology (5th. Edition). Pacific Grove, CA: Duxbury.
Zevin, J. D., & Seidenberg, M. S. (2002). Age of acquisition effects in word reading and other tasks. Journal of Memory and Language, 47, 1-29.

Posted in 14. Modelling - collinearity, collinearity, rstats | Tagged , , , , , , , , , , , | Leave a comment

Modelling – examination correlations: advanced scatterplots

Posted on May 4, 2013 by robayedavies

This post will focus exclusively on the relationships between pairs of variables. We will be looking at the item norms data, though you might want to practice the R procedures we deploy on the subjects data (see earlier posts here, here and here).

We will follow closely on the examination of variable distributions, that is, the characteristics of variation in items’ values on attribute variables like length in letters. We have previously discussed how to obtain the data here, how to draw histograms or density plots to examine variable distributions here, and how to compare the mean values of variables split (here) by item type, using the t-test, here.

What we are going to do here is to focus on the examination of whether – for any pair of variables – the variation in one relates to the variation in the other.

We will build on our previous work with scatterplots, which focused on the relationships between subject attribute variables (see here).

Visualizing the relationship between two variables

There is no point considering the relationship between two variables if values in the variables do not vary. We have had a look at the distribution of the item attribute variables, however, and we know that our items are pretty varied on length, orthographic neighbourhood size and bigram frequency.

Previous research (e.g. Baayen, Feldman, & Schreuder, 1997; Balota, Cortese, Sergent-Marshall, Spieler, & Yap, 2004; Weekes, 1997) shows how, most of the time, the length, orthographic neighbourhood size and the frequency of sub-lexical (we’ll focus on bigram) components of words correlate such that longer words have fewer neighbours and are composed of letters or letter clusters (e.g. bigrams) having lower average token frequency. As noted previously, this will make it tough to work out what the significant influence on reading performance might be, given a set of predictors that includes all these correlated variables. However, first, we’ll just concern ourselves with capturing the relationships between the variables.

We have seen how to produce a nice scatterplot showing the relationship between two variables, using code like this:


pdf("ML-data-item.norms-scatters-smoothers-edited-040513.pdf", width = 6, height = 6)

pln <- ggplot(item.norms,aes(x=Length, y=Ortho_N))
pln <- pln + geom_point() + ggtitle("Length x N-size")
pln <- pln + xlab("Item length in letters (jittered)") + ylab("Orthographic neighbourhood size")
pln <- pln + theme(axis.title.x = element_text(size=25), axis.text.x = element_text(size=20))
pln <- pln + theme(axis.title.y = element_text(size=25), axis.text.y = element_text(size=20))
pln <- pln + geom_smooth(method="lm", size = 1.5)
pln <- pln + theme_bw()
pln

dev.off()

To create a scatterplot like this:

R-6-1-scatter

Which shows us that:

—  Longer items have fewer neighbours: e.g. 3-letter items have between 3 and 20 neighbours, while 6-letter items have basically no neighbours.

— A number of items have exactly the same length and N-size values so the points are printed  one on top of the other.

When we have observations being printed one on top of the other, or otherwise when we have crowds of points that obscure the pattern in a plot i.e. the relationship between two variables, we have overplotting (see Chang, 2013; Wickham, 2009, for comments and alternate solutions to overplotting).

Here, we can deal with the fact that we have a number of points that all have the same length by adding a bit of random noise to their positions on the x-axis and y-axis, jittering, something we can have done for us by calling the geom_jitter() function to draw the scatterplot, as in:


pdf("ML-data-item.norms-scatters-smoothers-jitter-040513.pdf", width = 6, height = 6)

pln <- ggplot(item.norms,aes(x=Length, y=Ortho_N))
pln <- pln + geom_jitter() + ggtitle("Length x N-size")
pln <- pln + xlab("Item length in letters") + ylab("Orthographic neighbourhood size")
pln <- pln + theme(axis.title.x = element_text(size=25), axis.text.x = element_text(size=20))
pln <- pln + theme(axis.title.y = element_text(size=25), axis.text.y = element_text(size=20))
pln <- pln + geom_smooth(method="lm", size = 1.5)
pln <- pln + theme_bw()
pln

dev.off()

which gives us this:

R-6-2-jitter

Notice:

— The relationship is still there.

— The points are scattered about their ‘raw’ data original positions.

— Not everyone likes jittering but I think a jittered plot is more useful than one without, where one of the variables has a discrete values distribution resulting in the impression (misleading) that there are only a few observations because they are all printed on top of each other.

Just while we’re fancying up our scatterplots, it is worthwhile looking at this:

http://www.r-bloggers.com/2d-plot-with-histograms-for-each-dimension-2013-edition/

— Which shows us how to present a scatterplot and density distribution plots for each the two variables being examined.

— This version of the scatterplot requires that the gridExtra() package is installed and that the library for that package is then loaded before the code can be run.

The code, adapted from that given by Michael Kuhn at the URL above, is:


pdf("ML-data-item.norms-scatters-smoothers-jitter-density-040513.pdf", width = 6, height = 6)

p <- ggplot(item.norms, aes(x=Length, y=Ortho_N, colour = item_type)) + geom_jitter()

p1 <- p + theme(legend.position = "none")

p2 <- ggplot(item.norms, aes(x=Length, group=item_type, colour=item_type))
p2 <- p2 + stat_density(fill = NA, position="dodge")
p2 <- p2 + theme(legend.position = "none", axis.title.x=element_blank(),
 axis.text.x=element_blank())

p3 <- ggplot(item.norms, aes(x=Ortho_N, group=item_type, colour=item_type))
p3 <- p3 + stat_density(fill = NA, position="dodge") + coord_flip()
p3 <- p3 + theme(legend.position = "none", axis.title.y=element_blank(),
 axis.text.y=element_blank())

g_legend<-function(a.gplot){
 tmp <- ggplot_gtable(ggplot_build(a.gplot))
 leg <- which(sapply(tmp$grobs, function(x) x$name) == "guide-box")
 legend <- tmp$grobs[[leg]]
 return(legend)
}

legend <- g_legend(p)

grid.arrange(arrangeGrob(p2, legend, p1, p3, widths=unit.c(unit(0.75, "npc"), unit(0.25, "npc")), heights=unit.c(unit(0.25, "npc"), unit(0.75, "npc")), nrow=2))

dev.off()

And it delivers this scatterplot with density plots figure:

R-6-3-jitter-density

Which needs a bit of tidying up but is pretty awesome.

Notice:

— We simultaneously view the relationship between two variables and how these variables vary.

— Doing all this with a words vs. nonwords split.

— I don’t exactly understand everything in the code so will not explain it here but – I did understand it enough to adapt it for my own uses: if you compare my adaptation with Kuhn’s original, you should see what needs to be done to use it.

— How I would work out the function of the components would be by changing each, one by one, and seeing what resulted.

What have we learnt?

(The code for creating the plots drawn in this post can be found here.)

The key insight from drawing such plots is that for some pairs of variables variation in one, say, variation in length, is associated with variation in the other, say, orthographic neighbourhood size. There seems to be a systematic association. There are short and long items: that is what we mean by variation. On average, longer items have fewer neighbours: that is what we mean by systematic association. Of course, we will be testing this association formally using correlation, in a later post.

Key vocabulary

scatter plot

jitter

geom_jitter()
geom_point()
geom_density()

stat_density()

Reading

Baayen, R. H., Feldman, L. B., & Schreuder, R. (2006). Morphological influences on the recognition of monosyllabic monomorphemic words. Journal of Memory and Language, 55, 290-313.
Balota, D. A., Cortese, M. J., Sergent-Marshall, S. D., Spieler, D. H., & Yap, M. J. (2004). Visual word recognition of single-syllable words. Journal of Experimental Psychology: General, 133, 283-316.
Chang, W. (2013). R Graphics Cookbook. Sebastopol, CA: o’Reilly Media.
Weekes, B. S. (1997). Differential effects of number of letters on word and nonword naming latency. The Quarterly Journal Of Experimental Psychology, 510A 439-456.
Wickham, H. (2009). ggplot2: Elegant graphics for data analysis. Springer.

Posted in 12. Modelling - scatterplots+, modelling, rstats | Tagged , | Leave a comment

Modelling – examination correlations: combining dataframes

Posted on May 4, 2013 by robayedavies

This post will build on the previous Modelling posts. We are continuing to focus on the item norms data, previously discussed here and here (where I talked about were the data are from), here and here (where I talked about examining the distribution of variables like length) and here (where I talked about examining the relationships between pairs of variables.

I want to move on to examine the relationships between the variables corresponding to a larger set of item attributes than just the length, orthographic neighbourhood size and bigram frequency of items. The latter variables are measures that apply to words as well as to nonwords. I want to bring in variables capturing also, for each word: how common it is in our experience (frequency); how early in life we learnt it (age-of-acquisition, AoA); and how easy it is to imagine the referent or concept that the word names (imageability). There is an extensive literature on why these variables might be considered influential in an examination of variation in reading performance; interested readers can start with the recent papers examining the effects of these variables on observed reading behaviour (Adelman, Brown & Quesada, 2009; Balota et al., 2004;  Brysbaert & New, 2010; Cortese & Khanna, 2007).

We have data on the frequency, AoA and imageability measures in one data base, and on length, neighbourhood and bigram frequency in another.

The purpose of this post is to show how to put the databases together, and then modify them for our purposes.

Download the datafiles and read them into the workspace

As shown previously, we start by downloading the databases required:

We have .csv files holding:

1. data on the words and nonwords, variables common to both like word length;

2. data on word and nonword item coding, corresponding to item in program information, that will allow us to link these norms data to data collected during the lexical decision task;

3. data on just the words, e.g. age-of-acquisition, which obviously do not obtain for the nonwords.

Click on the links to download the files, then read them into the workspace using read(), as shown here.

We will be focusing on the dataframes:

item.norms

word.norms

There are 160 words and 160 nonwords in the items dataframe. The same 160 words are in the words dataframe. Critically,  the words are listed by name in the item_type column in item.norms and in the Word column in word.norms.

R-6-4-heads

We can use this common information as an index to merge the item and word norms data.

Rename variables

To merge two dataframes, there needs to be a common index in both. We have that common index but it has different names in the different dataframes. We solve this problem by renaming one of the variables using the rename() function from the reshape() package.


word.norms <- rename(word.norms, c(Word = "item_name"))

Notice:

— We are recreating the word.norms database from itself, with the rename() function call transforming the name of that name variable, capital W word.

— Don’t ask me why you need to put the old and the new column names in a c() concatenate function, I guess you might consider the pair of names to be a vector with two elements.

If you run that line of code, the renaming is done. Easy

R-6-5-rename

Check that the word names in the item_name column in each dataframe do match

Before we can merge the dataframes by the common index of word names, now item_name, we need to check that the columns do have all item word names in common.

As mentioned, there are 160 words in each dataframe. Name is, of course, a nominal variable, a factor. We can inspect the levels (here, the different names) in a factor using the levels() function.


levels(item.norms$item_name)

levels(word.norms$item_name)

Which will show you this:

R-6-8-levels

Can you see the problem?

The word false is “FALSE” in word.norms and in item.norms. Sometimes, you have “false” in one dataframe and “FALSE” in another. All this false-FALSE happened because some of the .csv files were prepared in excel and in excel false or true automatically get converted to FALSE and TRUE because they are words that are reserved to refer to logic values. If we merge two dataframes with “false” in one but “FALSE” in the other, this difference in case would count as a mismatch because “false” is not == to “FALSE”.

Read the R help on merge here. It is a powerful and useful function, well worth the effort.

However, you have to be careful.

In merge():

1. R examines the common columns in the two dataframes. I imagine a logical test is done, row by row: do the rows match on the common column, TRUE or FALSE?

2. The rows in the two data frames that do match on the specified columns are extracted, and joined together.

N.B. If there is more than one match, all possible matches contribute one row each. This can lead to you getting more rows than expected in the output dataframe from merger, i.e. some kind of row duplication occurs.

N.B. You can merge dataframes on the basis of more than one common index.

Any mismatch causes a problem when we try to merge the dataframes because observations pertaining to the mismatch index entry will simply be dropped.

In merging item.norms and word.norms the resulting dataframe will not include data on the nonwords simply because there is no match for the latter in the word.norms dataframe.

The merge() operation does not require the rows to be sorted or to occur in the same order.

Merge dataframes by the common variable item_name

Now we have two dataframes with a common index of item names, with all names matching at least for words, we can do the merger as follows:


# now can merge the two norms databases

item.words.norms <- merge(item.norms, word.norms, by = "item_name")

# and inspect the results

head(item.words.norms, n = 2)
summary(item.words.norms)
describe(item.words.norms)
str(item.words.norms)
length(item.words.norms)
length(item.words.norms$item_name)
levels(item.word.norms$item_name)

When we inspect the results, things look as expected – an important sanity check – as we can see by considering the results of the summary() call.

R-6-9-summary

Notice:

— We have 160 words and no nonwords in the new dataframe.

— We have both the items and the words data in the same dataframe.

— There are a bunch of missing values on the Cortese variables – where some words did not have values in those databases for those variables.

— Those missings led me to collect some imageability ratings (brookesIMG) and get the Kuperman AoA values for these words.

Create a csv file from this dataframe resulting from our various transform, rename, merge operations

Just as one can read.csv() an excel readable .csv file, one can output or write a .csv file.

I do not want to go through all the things I have done again, so I create a file out of the result of all these operations. N.B. I think I found out how to do this in Paul Teetor’s (2011) “R cookbook” but I also think the advice is, as usual, all over the web.


# we can write this dbase out to csv:

write.csv(item.words.norms, file = "item.words.norms 050513.csv", row.names = FALSE)

The csv file will then be found in your working directory.

Check it out, compare it to the original component word.norms and item.norms csv files.

What have we learnt?

(The code to run this data merger can be found here.)

We have learnt to rename a dataframe variable.

We have learnt to inspect then merge two dataframes on the basis of a common variable, here, an item name index.

We have learnt how to output the resulting dataframe as a .csv file.

Key vocabulary

rename()

levels()

merge()

write.csv()

Reading

Adelman, J. S., Brown, G. D. A., & Quesada, J. F. (2006). Contextual diversity not frequency determines word naming and lexical decision times. Psychological Science, 17 814-823.
Balota, D., Cortese, M. J., Sergent-Marshall, S. D., Spieler, D., & Yap, M. (2004). Visual word recognition of single-syllable words. Journal of Experimental Psychology: General, 133, 283-316.
Brysbaert, M., & New, B. (2009). Moving beyond Kucera and Francis: A critical evaluation of current word frequency norms and the introduction of a new and improved frequency measure for American English. Behavior Research Methods, 41(4), 977-990.
Cortese, M. J., & Khanna, M. M. (2007). Age of acquisition predicts naming and lexical-decision performance above and beyond 22 other predictor variables: An analysis of 2,342 words. The Quarterly Journal of Experimental Psychology, 60, 1072-1082.

Posted in 13. Modelling - merging data | Tagged , , | Leave a comment

Modelling – examining correlations: first, look at predictor distributions

Posted on May 4, 2013 by robayedavies

This post follows on from the previous post, concerning the examination of variable distributions.

It is always useful to plot the distribution of variables like item attributes e.g. item length in letters. One important benefit of doing so is identifying whether your dataset is in the shape you expect it to be in: identifying errors, of input or coding, should happen early in analysis so I urge you to plot and examine the plots of your data as soon as you get started.

However, psycholinguistics papers typically report stimulus characteristics in the form of a tabled summary of the means and SDs of the attributes of your stimuli, possibly broken down by item type (e.g. words vs. nonwords). In addition, reports of stimuli typically include the results of comparisons of the mean values of item attributes for each stimulus item type.

We can get the summary statistics for our item attribute variables using the handy psych package function describeBy(). In making that function call, we specify that we want the item norms data statistics split by item type. The R output can be converted into a table in a number of different ways. The easiest elegant method would be to writing your report in knitr all inside R-studio. The easiest horrible method, for someone writing a report in Microsoft Word, would be to paste the R output in a .txt document, open that document in excel, sort the formatting of the table out in excel, paste that table into Word as a bitmap. I use the horrible method all the time, because I haven’t yet learnt how to knit in R, though I will, because the horrible method is horrible.

Reporting the mean length etc. of the words and nonwords will not be enough. We also need to test the difference between the mean lengths etc. of the words and nonwords statistically. We can do this using the t-test, so long as the data distributions are ‘reasonably’ normal; if they are not, we might prefer to use non-parametric tests to compare means.

I am not going to get into the theory behind the t-test here, though I wrote a set of slides for  an undergraduate statistics class which can be accessed at this link.

https://speakerdeck.com/robayedavies/t-test

I recommend reading Howell (2002) if you are unsure about t-tests. I have never found a clearer exposition of the logic of the main statistical tests (except maybe in Jacob Cohen’s writings).

I will come back to this important and pervasive test statistic in another post.

The code that we use to both get the summary statistics and perform the t-tests is very concise.


describeBy(item.norms, group = item.norms$item_type)

will get you a table of all the summary statistics you might need:

R-5-10-summarystats

And we can test the difference between the mean values for words vs. nonwords on each item variable as follows:


t.test(Length ~ item_type, data = item.norms)
t.test(Ortho_N ~ item_type, data = item.norms)
t.test(BG_Sum ~ item_type, data = item.norms)
t.test(BG_Mean ~ item_type, data = item.norms)
t.test(BG_Freq_By_Pos ~ item_type, data = item.norms)

which will give us a series of results (output fragment – screenshot shown):

R-5-11-ttests

telling us that words and nonwords are not significantly different on mean length, orthographic neighbourhood size or any of the bigram frequency measures.

What have we learnt?

(The code for doing these statistics can be found here.)

It is very easy to statistically describe and then examine the distribution of variables in R.

Key vocabulary

describeBy()

t.test()

Reading

Howell, D. C. (2002). Statistical methods for psychology (5th. Edition). Pacific Grove, CA: Duxbury.

Posted in 11. Modelling - distributions, modelling, rstats | Tagged , , , | Leave a comment

Modelling – examining correlations: first, look at predictor distributions

Posted on May 4, 2013 by robayedavies

This post will take a more in-depth look at the relationships between variables.

A key property of experimental data is that we measure attributes – characteristics of people,  stimuli, and behaviour – and that those measurements (the numbers) vary. Numbers vary. That’s like saying ‘water is wet’. However, data analysis concerns the description and the explanation or prediction of that variation.

I feel like I’m channeling Andrew Gelman’s book with Deborah Nolan on teaching statistics, here.

Let’s examine the relationship between the item attribute variables, beginning by looking at how the item attribute numbers vary.

Variation in the values of item attributes

1. Let’s start a new .R script (see here): in R-Studio, keyboard shortcut CTRL-shift-N or cursor click File menu-new R script.

R-rstudio-1-3-script

2. Download the files: get hold of the data, discussed previously here, by clicking on the links and downloading the files from my dropbox account:

We have .csv files holding:

1. data on the words and nonwords, variables common to both like word length;

2. data on word and nonword item coding, corresponding to item in program information, that will allow us to link these norms data to data collected during the lexical decision task;

3. data on just the words, e.g. age-of-acquisition, which obviously do not obtain for the nonwords.

3. Copy these files into a folder on your computer – we’ll characterize it as the working directory (see here) and I will be using a folder I have called resource R public:

R-5-1-folder

Notice:

— I took a screenshot here of my Windows 7 windows explorer view of the folder. Things might look differently in different operating systems.

— In Windows, the address for this folder can be found by clicking on the down arrow in the top bar of the explorer window: C:\Users\p0075152\Dropbox\resources R public.

— Windows lists folder locations with addresses where locations are delimietd by “\” – in R, you need to change those slashes to “/”, see the code following.

4. To get the data files – the item norms .csv files – into R, I need to first set the working directory to this folder, and then run read() function calls, which I can do with this code (see here):


# set the working directory

setwd("C:/Users/p0075152/Dropbox/resources R public")

# read in the item norms data

item.norms <- read.csv(file="item norms 270312 050513.csv", head=TRUE,sep=",", na.strings = "-999")
word.norms <- read.csv(file="word norms 140812.csv", head=TRUE,sep=",", na.strings = "-999")
item.coding <- read.csv(file="item coding info 270312.csv", head=TRUE,sep=",", na.strings = "-999")

If you have put the files in the working directory that you then correctly specify (slashes forward in R, backward in Windows – address correctly given), and if the files are in that folder, and if you have correctly spelled the file names then you should see this:

R-5-2-readcsv

Notice the dataframes are now listed in the workspace window in R-studio.

5. We will then need to load libraries of packages (like ggplot2) – packages that were previously installed – to make their functions available for use (see here) using the code:


# load libraries of packages

library(languageR)
library(lme4)
library(ggplot2)
library(grid)
library(rms)
library(plyr)
library(reshape2)
library(psych)

6. As before (e.g. here or here), I can start by inspecting the dataframes using convenient summary statistics functions.


# get summary statistics for the item norms

head(item.norms, n = 2)
summary(item.norms)
describe(item.norms)
str(item.norms)
length(item.norms)
length(item.norms$item_name)

7. We can then plot the distribution of the values in these variables to show how the items vary in each of the attributes: item length in letters; orthographic neighbourhood size; and bigram frequency.

By distribution, what I am talking about is how many items have one or other value on each variable. Are there many words or nonwords that are four letters in length, or that have one or more orthographic neighbours?

A convenient way to examine the distributions of the values associated with our items for each variable is to plot the variable values in histograms. We can use the same sort of code that we used to plot the distribution of variation in participant attributes, see here.

One concern that I have is that the item norms attributes have similar distributions for words and nonwords in my stimulus set. Remember that the item.norms database holds data on 160 words and 160 nonwords that were selected to be matched to the words. If the words and nonwords are matched, their distributions should look similar: the peaks of the distribution (i.e. where most items are on length or whatever) should be in about the same place. Let’s start by looking at the distributions using histograms, with the plots drawn to show words and nonwords separately side-by-side.

A couple of lines of code will show us the distribution of word and nonword lengths for our stimuli:


# plot the distributions of the item norms variables for words and nonwords separately

pLength <- ggplot(item.norms, aes(x=Length))
pLength <- pLength + geom_histogram() + facet_wrap(~item_type)
pLength

Will get you this:

R-5-4-histograms

A few more lines of code will get you plots for each variable, printed out as a grid, to show all variables at once, output to a pdf for report. (I’m actually only going to bother to plot item length, orthographic neighbourhood size, and mean bigram frequency; you can practice this process by adding plots for the other variables.)


# plot the distributions of the item norms variables for words and nonwords separately

pLength <- ggplot(item.norms, aes(x=Length))
pLength <- pLength + geom_histogram() + facet_wrap(~item_type)

pOrtho_N <- ggplot(item.norms, aes(x=Ortho_N))
pOrtho_N <- pOrtho_N + geom_histogram() + facet_wrap(~item_type)

pBG_Mean <- ggplot(item.norms, aes(x=BG_Mean))
pBG_Mean <- pBG_Mean + geom_histogram() + facet_wrap(~item_type)

# plot the distributions of all the variables at once, all split by item type

# print plots to a grid

# print the plots to places in the grid - plots prepared earlier

pdf("ML-data-items-histograms-040513.pdf", width = 10, height = 15)

grid.newpage()

pushViewport(viewport(layout = grid.layout(3,1)))

vplayout <- function(x,y)
 viewport(layout.pos.row = x, layout.pos.col = y)

print(pLength, vp = vplayout(1,1))
print(pOrtho_N, vp = vplayout(2,1))
print(pBG_Mean, vp = vplayout(3,1))

dev.off()

The pdf of the plots will get created in the working directory folder, and will show you this:

R-5-5-histograms#

It looks like a did a pretty good job, even if I do say so myself, finding nonwords that are similar to the words on length, neighbourhood size, and bigram frequency.

The values on the item attribute variables vary such that the numbers of words that have lengths of 3, 4, 5 or 6 letters seem similar to the numbers of nonwords with these lengths. The same similarity in distributions appears to obtain for the other variables.

8. I find it a bit inconvenient having to look at two plots side-by-side to make the comparison between words and nonwords on variation in item attributes. It would be easier if I could superimpose one distribution on top of the other.

I could superimpose the histograms quite easily, mapping the item type to the colour of the histograms with code like this:


# would be easier to make the comparison between words and nonwords if
# we superimposed the histograms, which we can do like this:

pOrtho_N <- ggplot(item.norms, aes(x=Ortho_N, fill = item_type))
pOrtho_N <- pOrtho_N + geom_histogram(position = "identity", alpha = 0.4)
pOrtho_N

Notice:

— I repeat the plot name at the end to get it drawn within R-studio in the plot window

— I am mapping the item type (word or nonword) to the fill or colour of the bars in the histogram.

— I am superimposing the distribution plots with the argument position = “identity” in the geom_histogram() function call.

— I am making the histogram bars slightly transparent by modifying plot opacity with alpha = 0.4.

— And all that gets you this quite nice plot:

R-5-6-super-histograms

9. As it happens, I tend to prefer using density plots to examine data distributions.

Histograms and density plots both show the distributions of variables considered on their own. (See here for a nice tutorial: I’ll do my best to explain things in the following.)

In a histogram, the area of each bar is proportional to the frequency of a value in the variable being plotted.

A histogram shows you the frequency of occurrence of values for a variable, where values are grouped together in bins. Think about bins as divisions of the variable, values in the variable go from low to high numbers, and these values can be split into bins. You might have bins of values of a size equal to the total range of values (e.g. neighbourhood size ranges from 0 – 30) divided by 30, which here equals bins representing neighbourhood size increments of 1. Variable range divided by 30 is the ggplot2 default, and bin size can be changed. If you are plotting a histogram to show frequency counts, the height of the bars will equal the frequency of occurrence of values corresponding to that bin. You can see in the example that  we have rather a lot of items with between 0 and 5 neighbours. The area covered by the histograms is equal to the number of observations: we have 160 word and 160 nonword observations for each variable.

Rather than showing the frequency count, we could opt to have the histogram show the frequency density of our variables. The frequency density is the frequency of occurrence of a set of values (a bin of values) divided by the width of variation in that set (the bin width). We make the space filled by all the bars equal to one, so that the height of each bar equals the proportion of observations having a value encompassed by the corresponding bin.

Where numbers vary continuously, using histograms to plot the distribution of values might be felt to be misleading. Splitting the numbers into bins is a choice we make, or, if we rely on defaults for the calculation of bin widths, a choice that R makes. It might be better, then, to estimate the probability for our data that each value in a variable occurs. Density plots can be understood as showing smoothed histograms.

A little bit of research shows that density estimation is a big topic, see here, and I am going to keep things simple – so that I only say what I understand. I find Dalgaard’s (2008) book nice and clear on this and am merely going to paraphrase him here:

The density for a continuous distribution is a measure of the relative probability of observing  a value or getting a value close to x.The probability of getting a value in a particular interval is the area under the corresponding part of the curve.

Kernel density estimation (paraphrasing here) is a way to estimate the probability density function of a variable. You are estimating the probability of values in a population from your data sample. Density, remember, is how much or how how often a value or set of values occurs. So if we are estimating density we can do so using a kernel density estimator, combining the kernel (a positive function that integrates to one) and a smoothing parameter called the bandwidth. The larger the bandwidth, the more smoothing there is, and you can see this if you modify the bandwidth argument in a density plot.

That, I am afraid, is all I can find in my books so far. The honest direction, here, is given by Kabacoff (2011) who remarks that the mathematics of kernel density estimation is beyond the scope of our interest. But I regard this section as a to-be-continued entry, as I would like to understand things a bit better.

For now, let’s use the density plots to examine our variables, and leave understanding them more for another time.

You can understand the similarity of the histogram and density curve methods for examining the distribution of variables by superimposing one on top of the other. Here, I am adapting a solution given in Winston Chang’s (2012) R cookbook. The key point is that we are going to draw a histogram and a density plot of the same data distribution – how each variable varies – scaling the histogram so that it shows value density.


pOrtho_N <- ggplot(item.norms, aes(x=Ortho_N, y = ..density..))
pOrtho_N <- pOrtho_N + geom_histogram(fill = "aquamarine", colour = "grey60", size = .2)
pOrtho_N <- pOrtho_N + geom_density(size = 1.15)
pOrtho_N

If you run this code you will see this in the plot window:

R-5-8-hist-density

Notice:

— I mapped the density values for the variable to the y-axis for both the histogram and the density plot.

— I changed the colour of the fills and the borders of the bars for the histogram with the fill, colour and size arguments in the geom_histogram() function call.

— I also changed the size of the line drawn to show the density estimate, to make it bolder, using the size argument in the geom_density() call.

— You can see how the occurrence of different values in this variable, orthographic neighbourhood size, for my sample of words and nonwords, has a big bump around 0-5 neighbours, as shown in the peaks of both the histogram and density plots of the data distribution.

We can redraw the side-by-side histogram plots using superimposed density plots to show how words and nonwords vary on each item attribute variable.


# now draw a grid of density plots
# plot the distributions of the item norms variables for words and nonwords separately

pLength <- ggplot(item.norms, aes(x=Length, colour = item_type))
pLength <- pLength + geom_density()

pOrtho_N <- ggplot(item.norms, aes(x=Ortho_N, colour = item_type))
pOrtho_N <- pOrtho_N + geom_density()

pBG_Mean <- ggplot(item.norms, aes(x=BG_Mean, colour = item_type))
pBG_Mean <- pBG_Mean + geom_density()

# plot the distributions of all the variables at once, all split by item type

# print the plots to places in the grid - plots prepared earlier

pdf("ML-data-items-densities-040513-wide.pdf", width = 24, height = 8)

grid.newpage()

pushViewport(viewport(layout = grid.layout(1,3)))

vplayout <- function(x,y)
 viewport(layout.pos.row = x, layout.pos.col = y)

print(pLength, vp = vplayout(1,1))
print(pOrtho_N, vp = vplayout(1,2))
print(pBG_Mean, vp = vplayout(1,3))

dev.off()

Which will produce a pdf that looks like this:

R-5-9-density

Notice:

— I adjusted the grid to show the density plots in a wide strip rather than a vertical one, because I think it looks better.

— It does not really make sense to present a density plot for a variable with discrete values, like Length, so I might prefer there to use a histogram instead.

What have we learnt?

(The code used to draw the plots in this post can be downloaded from here.)

We have examined how the items in our sample of words and nonwords vary in the item attributes.

We have looked at this variation in terms of the distribution of values in each variable.

We have examined distributions using both histograms and density plots, going a bit into what these plots represent.

Key  vocabulary

geom_density()

geom_histogram()

Reading

Chang, W. (2013). R Graphics Cookbook. Sebastopol, CA: o’Reilly Media.
Dalgaard, P. (2008). Introductory statistics with R (2nd. Edition). Springer.

Posted in 11. Modelling - distributions, modelling, plotting data, rstats | Tagged , , , , , | Leave a comment

Modelling – examining the correlations between predictor variables

Posted on May 3, 2013 by robayedavies

This post will consider how to explore the relationship between a set of variables: variables that we will ultimately use in a mixed-effects analysis of lexical decision data.

Most of the analyses we will be doing will examine whether observed reading behaviours e.g. the accuracy or latency of responses in experimental tasks like lexical decision are influenced by the attributes of the stimuli presented to participants, by the attributes of the participants themselves, or by interactions between the item and participant attributes.

By attribute I mean things like word length or frequency, or participant age or reading ability.

A concern in the analysis of psycholinguistic data is the way in which everything correlates with everything else. Thus, longer words typically look like few other words, words used more often in the language are learnt earlier in life, while older readers have read more print and are more skilled readers. These correlations are to be expected (that is not to say that we should not seek to explain them) but make things difficult when we are attempting to analyse data statistically.

You can understand the problem in terms of overlap. If you want to know what the effects of two attributes are, but these variables are correlated so that, essentially, the information provided by one variable overlaps with the information provided by the other, you are going to have a problem, and that problem is called multicollinearity.

As Cohen, Cohen, Aiken and West (2003) note, the estimate of the effect of one predictor will be unreliable because, if it overlaps with another predictor, little unique information will be available to estimate its value.

Think of it like this:

overlap-images-CC-National-Media-Museum

Creative Commons – flickr – National Media Museum: Elderly couple with a young female spirit

Creepy, right?

What are we looking at, which image is ‘real’?

Reading

I very much recommend reading the following publications to build understanding. I would start with Cohen et al. before going aware near Belsley et al (the authoritative text).

Baayen, R. H. (2008). Analyzing linguistic data. Cambridge University Press.

Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. New York: Wiley.

Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioural sciences (3rd. edition). Mahwah, NJ: Lawrence Erlbaum Associates.

Posted in 10. Modelling - collinearity, modelling, rstats | Tagged , , , | Leave a comment

Modelling – moving on

Posted on May 3, 2013 by robayedavies

girl-trampolining-CC-Florida-Memory

Creative commons – flickr – Florida Memory: Young girl jumping on a trampoline at the Sarasota High School Sailor Circus

We are now going to move into a new phase for these posts.

We are heading toward a consideration of correlation and regression, as base camp for further development towards mixed-effects modelling.

The next post will focus on correlations, previously mentioned here (where you’ll find a link to some slides) and the representation of relationships between variables (see here), making use of some of the selection or subsetting capability which we have just been developing (see here).

Posted in .Interim directions, image, modelling, rstats | Leave a comment

Getting started – it can be worrying

Posted on May 3, 2013 by robayedavies

bridge-mystery-CC-Florida-Memory

Creative commons – flickr – Florida Memory: Bridge over Homosassa river

One reason I am writing the blog is that when I started things were pretty mysterious. I knew I had to travel down the road but I wasn’t sure exactly where I’d end up or how I would get there.

There is plenty of guidance out there, but in case this is where you’ve ended up, I’ll try to be useful.

 

Posted in getting started, image, rstats | Leave a comment