Getting started – why bother?

Posted on May 3, 2013 by robayedavies

swimming-hole-CC-Florida-Memory

Creative commons – flickr – Florida Memory: View of the Blue Hole swiming area at Florida Caverns State Park

I sometimes recall an article by Jerry Fodor in, I think, the New York Review of Books where he asked himself (something like) “I could be out on a lake in my boat, why am I bothering to discuss modularity?”

I then think about the swimming spot I visited last summer, near Durango (Colorado), cold clear ice melt and hot (I mean 35+C) weather.

I found this picture on flickr and it shows the nearest approximation I found to the inviting quality of that remembered swimming in Colorado.

Anyway, let’s talk next about scatterplots again, but raise the level a bit and get into scatterplot matrices.

Posted in getting started, image, rstats | Leave a comment

Getting started – referring to dataframe elements by place, name or condition – selecting elements to subset data

Posted on May 3, 2013 by robayedavies

In the previous post, we revised how to read in dataframes (see also how to read in .csv files as dataframes), using the item norms database as an example (see also here), and we also revised how to get summary information on your dataframe.

We added new understanding by looking at how you can refer to a dataframe variable by name, using the dataframe.name$variable.name notation, which will be useful.

We looked at why as well as how you look at a dataframe – hint: its about making sure your data are in the shape that you think they are.

And, we looked at how you can test for and convert the type of a variable.

In this post, we will be doing all new work on how you refer to elements in a dataframe by place, name or condition.

This will help us to get to the really useful capacity to subset data.

In the next posts, we will look at how you subset a dataframe to help plotting and statistical analysis.

I recommend R-in-Action (Kabacoff, 2011; chapter 4) or the Quick-R website as a companion for this post.

OK, so we have the dataframe item.norms in our workspace, what’s in it?

R-4-9-summary

Notice:

— We previously played with converting the BG variables into factor variables then back into numeric variables using as.factor() and as.numeric(). As I am writing the previous post and this post in the same R session, the variables are still being treated as numbers.

— This conversion is not permanent but if you wanted to create a dataframe with the variables converted permanently, I think you would have to output the new dataframe using the write() function, which we will get to.

Referring to elements of a dataframe by place

You can refer to and interact with variables (columns) and observations (rows) and elements (a specific observation or observations in a specific variable or variables) by place, name, or conditionally (by examining a dataframe for if elements meet criteria you set). This is a big area but it is useful to get a flavour now.

Remember that head() will get you a view of the top rows in a dataframe.

R-4-8-head

You have seen [] before. In both matrices and dataframes, every element – every cell in a spreadsheet – can be located by the column it is in and the row it is in.

The notation used here is: dataframe[row index, column index]

Dataframe columns and rows are indexed by number:

1- x from left to right among columns;

1 – x from top to bottom among rows.

Let’s try this out using the example item.norms dataframe.


# let's look at the dataframe

head(item.norms, n = 2)

# what is the second variable (column)?

item.norms[, 2]

# what is the second observation (row)?

item.norms[2, ]

# what is the second observation in the second variable?

item.norms[2, 2]

Notice:

— If I am selecting columns, I specify which columns I want but leave the entry blank on rows: [ , which columns].

— If I am selecting rows, I specify which rows I want but leave the entry blank on columns: [which rows, ].

— If you run this code, you will see that “ask” is the entry in the second row of the second column (item names).

— This is not that hard to find out by eye when using excel or SPSS to look at a spreadsheet.

— The use of indices in R becomes extremely useful when you are dealing with larger data sets.

Subsetting dataframes

Let’s take this out for a walk.

I often get datasets where I might want to use only some of the variables (not others) or some of the observations (not others). There are a number of ways I can subset the dataframe.

Subsetting dataframes using the column or row indices

I can select a range of variables or rows by specifying them using the [] notation. I could ask for a set of variables (or observations) by defining a vector of columns (or rows) using the – c(x:y) i.e. from x to y or c(x,y,z) i.e. just x, y and z – notation for creating vectors that we saw earlier here and here. I could delete variables by adding – to the front of column or row indices. I would tend to create a new dataframe from the dataframe I am subsetting, to stay safe.


# I can subset the dataframe using the column or row indices

head(item.norms, n = 2)

# what if I just want the numeric variables?

new.item.norms <- item.norms[, c(3:7)]

head(new.item.norms, n = 2)

# what if I just want the Length and BG_Sum variables?

new.item.norms.2 <- item.norms[, c(3, 5)]

head(new.item.norms.2, n = 2)

# what if I just want the the top ten rows in the dataframe?

new.item.norms.3 <- item.norms[c(1:10),]

head(new.item.norms.3, n = 2)
summary(new.item.norms.3)

# what if I want to get rid of a variable?

# what if I want to get rid of the BG_Mean and item.name variables

new.item.norms.4 <- item.norms[,c(-2, -6)]

head(new.item.norms.4, n = 2)

# use the - operator to get rid of rows also

Notice:

— I might set conditions on

Using the column and row indices is useful.

Generally, however, I tend to prefer selecting variables by name and rows by condition.

Subsetting variables by name

I prefer to subset variables by name because I often deal with dataframes with many (20+) variables and counting the variables to find the right number is both costly and susceptible to error. Better to select variables by name. Obviously, you need to enter the name correctly, so I often copy/paste the name from the output of a head() call in the console into the script window.

Note that in the following I change how I get rid of variables.


# I can subset the dataframe using the column names

head(item.norms, n = 2)

# what if I just want the numeric variables?

new.item.norms.5 <- item.norms[, c("Length", "Ortho_N", "BG_Sum", "BG_Mean", "BG_Freq_By_Pos")]

head(new.item.norms.5, n = 2)

# what if I just want the Length and BG_Sum variables?

new.item.norms.6 <- item.norms[, c("Length", "BG_Sum")]

head(new.item.norms.6, n = 2)

# what if I want to get rid of a variable?

# what if I want to get rid of BG_Mean and item.name variables?

dropvars <- names(item.norms) %in% c("item_name", "BG_Mean")

new.item.norms.7 <- item.norms[!dropvars]

head(new.item.norms.7, n = 2)

Notice:

— In removing variables, I adapted code in R-in-Action (Kabacoff, 2011; p.87):

1. I created a vector of variable names, dropvars, using names(item.norms).

2. names(item.norms) %in% c(“item_name”, “BG_Mean”) created a logical vector with TRUE for each element in names(item.norms) that matched the item_name and BG_Mean variable names, FALSE otherwise.

3. The ! operator reverses those logical values.

4. item.norms[!dropvars] selects columns with TRUE logical values i.e. all except the item_name and BG_Mean variables.

— Pretty nifty, right?

Subsetting observations by condition

I do not usually select observations (rows) by index, I usually subset observations that meet conditions I specify.


# selecting observations by condition

# item.norms holds data on both words and nonwords, what if I want# to focus on just words?

item.norms.words <- item.norms[item.norms$item_type == "word", ]

summary(item.norms)
summary(item.norms.words)

# what if I want to focus on just words of length 3 letters?

item.norms.words.3 <- item.norms[which(item.norms$item_type ==
"word" & item.norms$Length == 3), ]

summary(item.norms)
summary(item.norms.words.3)

Notice:

— In the first example, I am specifying a condition on rows, leaving the entry blank on columns.

— In setting the condition, I am asking R to select those observations that meet the condition that the item_type value is word. This is a logical comparison and I use the logical operator == which means ‘equal to’ or ‘is the same as’.

— What we are doing here is selecting rows according to a logical test: “Is the observation associated with a value on item.norms that is exactly equal to ‘word’? TRUE or FALSE?”

— In R, = means the same as the <- assignment arrow i.e. you are assigning a value to an object name. If all you are doing is asking if something meets a condition (is the same as) then you use ==.

A useful primer on R operators can be found in Quick-R, here.

— In the second example, I am following an example used by Kabacoff (2011; p. 87).

— I am setting two conditions, that there is a subset of just words, and only those words that are three letters in length.

— We break the effect of the code down as follows (see Kabacoff, 2011; p. 87):

1. The logical comparison item.norms$item_type == “word” produces a vector of logic values, TRUE if the observation is about a word, FALSE if it is not: the vector will have as many elements as there are items in item.norms.

2. The logical comparison item.norms$Length == 3 does the same kind of thing, producing a  vector of logical values, TRUE if the item has a length of 3.

3. The & (logical AND) operator combines the two so that a vector is produced if and only if the item is both a word and has a length of 3.

4. The function which() tells us which elements of the joint condition logical vector are TRUE, i.e. indexing where items are words and have length 3.

5. The item.norms[which(…), ] call selects those rows corresponding to the which() index.

Again, this is very neat.

I used to select items in excel by sorting rows but that invited errors (did I sort all the rows?) and was not self-annotating i.e. reproducible, as an operation coded in a .R script is.

I think you can also do this in SPSS but I don’t know because, frankly, doing it in R is easy and safe, so why bother to learn how to do it in SPSS?

How to subset data using the subset() function

I now often use the subset() function to do much of what I have shown in the foregoing.


# selecting variables or observations using the subset() function

head(item.norms, n = 2)

# what if I just want the numeric variables?

new.item.norms.8 <- subset(item.norms, select = c("Length",
"Ortho_N", "BG_Sum", "BG_Mean", "BG_Freq_By_Pos"))

head(new.item.norms.8, n = 2)

# what if I want to get rid of the BG_Mean and item_name variables

new.item.norms.8 <- subset(item.norms, select = -c(BG_Mean,
item_name))

head(new.item.norms.8, n = 2)

# selecting observations by condition using subset()

# item.norms holds data on both words and nonwords, what if I want# to focus on just words?

item.norms.words.4 <- subset(item.norms, item_type == "word")

summary(item.norms)
summary(item.norms.words)

# what if I want to focus on just words of length 3 letters?

item.norms.words.5 <- subset(item.norms, item_type == "word" &
Length == 3)

summary(item.norms)
summary(item.norms.words.5)

As you can see, the syntax involved in using subset() is a bit simpler.

Notice:

— Selecting variables and rows is very easy.

— Using code to do this makes the changes between dataframes reproducible.

— Using this R code is neat, and given its flexibility, powerful.

What have we learnt?

[The code used for this post can be found here.]

We have learnt to refer to elements by row and column indices, using the [,] notation.

We have learnt to select variables by place index, or name.

We have learnt to select observations by place index or condition.

We have learnt how to remove variables or observations.

We have learnt how to use the subset() function to do all these things.

We have also learnt about logical operators.

Key vocabulary

[,]

which()

%in%

:

&

!

–

==

subset()

Posted in 9. Getting started - subset, getting started, rstats, subset | Tagged , , | Leave a comment

Getting started – basics: vectors and matrices; creating them; manipulating them; referring to specific elements in them

Posted on April 30, 2013 by robayedavies

We looked previously at data structures like vectors, and data types or modes, as in numeric, character string or logical. I’ll recap some of the previous post on vectors and then move on to talking about data structures like matrices (this post), and data frames (in brief here, in detail next post). This is because where we’re going we’ll need to know about things, and where we’re going is to the capacity to be able to create and manipulate data structures. (Other data structures, arrays and lists, will appear later.)

Data structures

The entities that R creates and manipulates are known as objects. These may be variables, arrays of numbers, character strings, functions, or more general structures built from such components.

R introduction

During an analysis, an object is created, stored and used by name.

You can create and use objects – data structures – such as scalars, vectors, matrices, arrays, dataframes, and lists.

Vectors

Vectors are one-dimensional arrays that can hold numbers, words, or logical data (Kabacoff, 2011; p. 24). Note that vector elements can have only one mode i.e. be data of one type only.

You can create a vector using the concatenate or combine function c().


# a vector of numbers

A <- c(1,2,3,4,5)

# a vector of character strings

B <- c("a", "b", "c", "d", "e")

# a vector of logical values

C <- c(TRUE, TRUE, TRUE, FALSE, FALSE)

Notice:

— I am putting the characters in quotation marks when I create vector B. You will see everywhere in R that character strings (from elements of data, as in the example, to plot titles) are entered using either matching double (“) or single (‘) quotes but are printed using double quotes or sometimes without quotes (see here).

You can create vectors using also the functions seq() and rep(). You use seq() to get a sequence of numbers separated by equal steps


D <- seq(1,5)

E <- seq(100,500,100)

Notice:

— The first function call, C <- seq(1,5), asked for a sequence of numbers from 1 to 5 in steps of 1: the default step size of 1 is used unless we add an argument to the seq() function call.

— the second call, D <- seq(100,500,100), asked for a sequence of numbers from 100 to 500 in steps of 100.

We could alternatively do the first kind of operation using the : operator e.g. e <- 10:50.

Notice:

— The seq() function affords greater flexbility.

The replicate rep() function allows you to create a generate repeated values. You might want to use this function if you were generating some coding values for a dataset. Let’s say you had a set of five observations all of which had been recorded by a researcher named RA, you could add a variable coding for the researcher’s identity by using rep(). What if you wanted to code for the presence of a feature, the feature is either there (code as 1) or not (code as 0) and it is there for the first three but not the second observations, you can create a vector of numbers doing the coding also using rep().


RA.ID <- rep("RA", 5)

coding <- rep(1:0, c(3,2))

Vectors are objects and you can interact with them. You can refer to specific elements in a vector using a vector.name[] position notation.

I mean, you can ask what the fourth element in a vector is by asking for it with C[4], or you can ask what the first and second elements in a vector are by asking for them with B[c(1,2)].


C[4]

B[c(1,2)]

Notice:

— You will see c(), seq(), [], over and over again in R code.

Matrices

A matrix is a two-dimensional array where each element has the same mode, whether that be number, character or logical. I will be brief here because matrices are important to the statistical analyses you will use, and thus in how R works, but will not often be created directly by you.

Matrices can be created with the matrix(), cbind() and rbind() functions. I use the latter all the time so you’ll see them again. We might use matrix() again, I suspect for plotting model predictions, so need to at least lay out the basics here.

When using matrix(), you define a vector of values, then define how you want the matrix structured – how many rows, how many columns – then you define how you want the values put into the matrix structure; the default is by columns, but you could have it by rows.


# create a vector of numbers

F <- seq(1,20)

# create the matrix, with 5 rows and 4 columns

G <- matrix(F, nrow = 5, ncol = 4)

# same numbers, but different dimensions

H <- matrix(F, nrow = 4, ncol = 5)

# same numbers, 5 rows and 4 columns, but filled by rows rather
# than by (default) columns

I <- matrix(F, nrow = 5, ncol = 4, byrow = TRUE)

Try these bits of code out.

You can also create matrices by sticking vectors together using the column bind cbind() and row bind rbind() functions.

As noted, you will use these functions over and over again because you can bind not only vectors – as in these toy examples – but big, complicated, datasets (dataframes) using the exact same functions. It beats copy and paste in excel or SPSS.

We can exemplify the use of the functions with the vectors we have already created.

You can rbind() the vectors D and E together to create a matrix J with 2 rows and 5 columns. You can cbind() the vectors D and E together to create a matrix K with 5 rows and 2 columns


J <- rbind(D,E)

K <- cbind(D,E)

Try these bits of code out.

Obviously, here, R does not know whether the vectors are ‘horizontal’ or ‘vertical’:  both are just a string of numbers which could be either so the rbind() and cbind() calls are what determine whether you get a 2 x 5 or a 5 x 2 matrix of values.

Matrices have dimensions i.e. in the examples G is 5 x 4 matrix while H is 4 x 5.

The rbind() and cbind() functions will not succeed if the numbers of elements do not match, whether by row or by column, and you will get an error message tell you that the number of columns or rows must match, as you’ll see if you try this incorrect function call:


L <- rbind(G,H)

That will get you the error: ” Error in rbind(G, H) : number of columns of matrices must match (see arg 2) ”

Thus, to get rbind() to work: make sure that the number of columns for the matrices you are trying to bind do match, or make sure that the vectors you are trying to bind have the same number of elements, or that the vector you are trying to bind to a matrix has the same number of elements as the matrix has columns.

Obviously, the same restriction will apply to using cbind().

I can rbind() correctly the G and I matrices because they both have the same number of columns since they are two 5 x 4 matrices. I can cbind() the G matrix and the E vector because E has as many elements as G has rows.


L <- rbind(G,I)

M <- cbind(G, E)

Notice:

— We cannot add values of a different data mode i.e words to a number matrix, as in:

N <- cbind(M, RA.ID)

— The function call will work but everything in the matrix will now be treated as a word or character string.

— If you want to have numbers and words in the same data table you will be working with dataframes, which we will focus on in the next post, and treat briefly here.

Matrices and referring to specific elements using subscripts

Here comes something really useful, that will remain useful throughout your R career.

You can identify rows, columns, or elements of a matrix by using the []  subscript notation available in R (Kabacoff, 2011; p. 25).

I cannot over-emphasize how handy this is.

We can take one of the matrices we have built as an example in the foregoing, M. In creating M we put together a 5 x 4 matrix of numbers from 1:20 (G) with a vector of numbers from 100 – 500 (G). It looks like this:

R-4-5-matrix

Notice:

— I did not bother to name the rows or columns of the 5 x 4 matrix G, so R has supplied column names V1-4 and row names 1-5; obviously, vector E will get its name carried with it into the matrix M I created through cbind().

Anyway, for matrix M, I can refer to specific elements of the matrix by position using a subscript notation.

X[i,] refers to the ith row of matrix X.

X[,i] refers to the jth column of matrix X.

X[i,j] refers to the element at the ith row and jth column of X.

You could refer to multiple elements by entering a vector.

X[i, c(1,3)] refers to the 1st and 3rd elements at the ith row of X.

Now see how we can find out to use this notation to select – have reported to us – specific elements in a matrix.


# get the 2nd row in M

M[2,]

# get the second column in M

M[,2]

# get the element in the second row, second column in M

M[2,2]

# get the elements 1 and 3 in the second row in M

M[2,c(1,3)]

Run the code and verify that the answers are correct.

Dataframes

I have mentioned dataframes before, here and elsewhere. As I have noted, they are what we will be dealing with most of the time, and they will appear most familiar to you, similar to the tables or sets of data you have used in SPSS or excel. You will know, from your experience, that you can get all different kinds of words into excel and (with restrictions i.e. specifying variable data types) into SPSS.

A dataframe is like a matrix. There are rows and columns of values. You can specify or work with specific elements in the dataframe using the [i rows, j columns] notation. You can work with dataframes using the cbind() and rbind() functions.

A dataframe is more general than a matrix because different columns can hold different kinds of data i.e. include variables with number values, or character etc. values.

You can create a data.frame using the data.frame() function.

Thus, if we just cbind() a matrix M of numbers and a vector RA.ID of character strings, we produce a matrix of character strings (all numbers get treated as characters by R).

While if we use data.frame() to put M together with RA.ID, we get a set of observations including both a vector of characters and a set of numbers.


# use cbind() to create a matrix of characters from a matrix
# of numbers and a vector of characters

N <- cbind(M, RA.ID)

# we can create a dataframe using the data.frame() function:

O <- data.frame(M, RA.ID)

And you can see the difference in the way that R treats the objects N and O in how they are listed in the workspace window in R-studio, N as a matrix of characters, and O as a data.frame of 5 observations with 6 variables.

R-4-6-dataframe

Notice: the difference in the listing on the right here.

What have we learnt?

[The .R script used in the examples can be downloaded from here.]

We have learnt about data structures, especially vectors, matrices and dataframes.

We have learnt how to create vectors, and how to refer to specific elements in a vector by position.

We have learnt how to create matrices, and how to refer to specific elements by position using the [] notation.

We have learnt about dataframes as a more general form of matrix.

Key vocabulary

c()

seq()

: operator

rep()

cbind()

rbind()

matrix()

[,] notation

data.frame()

Reading

The things treated here are very useful, so bear further study. There are clear chapters on this material in Kabacoff (2011) and Dalgaard (2008) – books that I recommend – among other sources.

Posted in 8. Getting started - data, getting started, rstats | Tagged , , , , | Leave a comment

Getting started – recapping basics, adding foundational knowledge

Posted on April 27, 2013 by robayedavies

This post assumes that you have installed R and R-studio, see here and here if not.

Getting started with data analysis can require a shift in mind-set.

Home base for most people is a spreadsheet

Most people find it difficult to start using R because they are most comfortable with something that resembles a physical version of their data, an SPSS or excel spreadsheet.

I assume you have seen a spreadsheet of data looking like this:

R-3-1-SPSS

Notice:

— You can see a table of columns and rows. The columns have names like Length and the rows have numbers (on the far left).

— At the intersection of each column and row there’s a cell.

— There are scroll bars on the right, for vertical scrolling, and at the bottom, for horizontal scrolling.

This is SPSS but excel will show you something similar if you open an .xlsx spreadsheet. You can move around it and interact with it like any other thing in the world. Except, of course, it would be a mistake to think of a spreadsheet like that because what counts is the information, and the capacity to address, manipulate and analyse it.

R basics – the data objects

I have referred previously to the R workspace, objects, dataframes and variables, as here and here, where we read in a data file on participant scores in reading and other tests for a reading experiment, and drew some plots like histograms and scatterplots.

Before we go on, we need to firm up our understanding of how data are represented and analysed in R.

R is a language and you learn that language to create and manipulate objects (see the R intro). During data analysis, objects are created and stored by name.

[Think about the cultural difference here, compared to SPSS and excel: sure, in those applications, you call your data files and your variables by name but, because you can scroll around the data files i.e. spreadsheets, the variable names you use can be useless (meaningless, imprecise, poorly remembered etc.) but that need not stop you because they are things with locations in a field (the spreadsheet) and you can find a datum in a .sav or .xlsx file simply by looking, just as you can see a poppy in a wheat field even when ignorant of its name.]

The collection of objects currently stored is the workspace. You might keep data files in a folder on your computer, and you will direct R to that folder as a working directory, using the setwd() function. But you will load data files (e.g. a .csv file) using the read.csv() function — or some other version of read() — stored in the working directory to make them available to R as objects in the workspace. (Got it? See this Quick-R post for help.)

If you’re using R you’re dealing with data.

Data structures and data modes

R deals with data in a variety of types or structures: scalars, vectors, arrays, matrices, dataframes and lists. This diversity is one reason R is so flexible, and thus, powerful.

A dataframe is equivalent to the spreadsheet in SPSS or excel: a rectangular collection of data arranged in columns (variables or attributes) and rows (observations or cases)

There are different structures but also different data types or modes. R can deal with: numeric, character, logical and other types of data.

mode-CC-US-National-Archives

[Search “mode” in flickr Creative Commons and this what you get, US National Archives: mounted horsemen, awaiting the start of a parade, Cotton Wood Falls, Kansas, 1974]

The entities R operates on are objects. Objects have properties (or attributes) like their mode or length.

Vectors

You could have a chain or sequence or one-dimensional array of numbers or logical values or words (character strings): a vector of numeric values; logical values or character strings.

Vectors must have their values all of the same mode. A vector can be empty and still have a mode.

You can create a vector using the c() function: I think c means concatenate i.e. to chain things together.


# data basics - vectors, arrays, matrices, dataframes ###################################################

# make a vector using c()

# a vector of numbers

x <- c(1,2,3,4,5)

# a vector of words or character strings

y <- c("the", "cat", "sat", "on", "me")

# a vector of logical values

z <- c(TRUE, TRUE, FALSE, TRUE, FALSE)

# making a vector of numbers by generating a sequence of integers
# note the use of the colon : operator

a <- seq(10:15)

If you run this code in R, you can see each vector being listed in the workspace as an object – vectors of varying mode – after the function call.

R-4-3-vector-modes

The data in a vector must be of only one type or  mode.

Scalars are vectors of one element, and are used to hold constants.

You can interact with the vectors – they are objects.

You can refer to an element by place or position, specifying place by number within square brackets. For example, for the vectors produced in the foregoing, the fourth place element is, or the first and the second elements are:


x[4]
y[4]
z[c(1,2)]

Run those lines of code and you’ll see:

R-4-4-vectors

Matrices

Arrays

Dataframes

— to follow

There are also objects called lists with the mode list. These are ordered sequences of objects which can each be of any modes (including list – you could have a list of lists).

Further reading

Read the R-in-Action book or the Quick-R blog, or indeed the R introduction, for further help but, honestly, the information you need is all over the internet.

Posted in 8. Getting started - data, getting started, rstats | Tagged , , , , , | Leave a comment

Getting started – selecting data, wrangling data – early (basic) moves

Posted on April 24, 2013 by robayedavies

This post and the few following will switch focus from the ML subject scores database to a database built out of normative data about word attributes, which actually comes in a number of different parts (downloadable at the links). Remember that these data are about the stimuli presented in a lexical decision test of visual word recognition and therefore include information about words and a matched set of nonwords.

We have .csv files holding:

1.data on the words and nonwords, variables common to both like word length;

2. data on word and nonword item coding, corresponding to item in program information, that will allow us to link these norms data to data collected during the lexical decision task;

3. data on just the words, e.g. age-of-acquisition, which obviously do not obtain for the nonwords.

These databases will be put together, manipulated and otherwise wrangled to achieve good understanding and an appropriate format for analysis of the word recognition behaviour recorded.

The normative data (e.g. frequency values etc. rather than item coding) were extracted from the English Lexicon Project (ELP, Balota et al., 2007) or from collections of ratings data reported and made available by Cortese and colleagues (Cortese & Fuggett, 2004; Cortese & Khanna, 2008) or by Kuperman and colleagues (Kuperman et al., in press). The repositories for the data can be found at the ELP website or at the locations specified in the cited papers. The normative data are available in the downloadable files here only to illustrate how to interact with such data in R.

References

Balota, D. A., Yap, M.J., Cortese, M.J., Hutchison, K.A., Kessler, B., Loftus, B., Neely, J.H., Nelson, D.L., Simpson, G.B., & Treiman, R. (2007). The English lexicon project. Behavior Research Methods, 39, 445-459.

Cortese, M.J., & Fugett, A. (2004). Imageability Ratings for 3,000 Monosyllabic Words. Behavior Methods and Research, Instrumentation, & Computers, 36, 384-387.

Cortese, M.J., & Khanna, M.M. (2008). Age of Acquisition Ratings for 3,000 Monosyllabic Words. Behavior Research Methods, 40, 791-794.

Kuperman, V., Stadthagen-Gonzales, H., & Brysbaert, M. (in press). Age-of-acquisition ratings for 30 thousand English words. Behavior Research Methods.

Posted in .Interim directions, getting started, rstats | Tagged , , | Leave a comment

Getting started – what’s next?

Posted on April 23, 2013 by robayedavies

We will switch databases, to a set of data on item attributes.

IMG_0819

And we will work on another of the especially attractive and powerful features of R: the capacity to select and work with specific elements of a larger database: subsetting rows and columns by number or place, name, and condition.

Then we’ll use subsets of the item attribute data to further examine correlations between variables.

This will start to prepare us for linear regression.

And that will lead up to mixed-effects modeling.

Posted in .Interim directions, getting started, image | Leave a comment

Getting started – statistical concepts – correlations

Posted on April 23, 2013 by robayedavies

As we advance through the capabilities of R, we will increasingly take on the development of understanding of key statistical concepts.

I have uploaded some undergraduate-level slides on correlations here:

— check them out or, better, read a chapter on correlations and regressions in any statistics or data analysis text book.

Posted in modelling, rstats | Tagged , | Leave a comment

Introduction to DMDX, R and reproducible research in psycholinguistics – some proselytizing

Posted on April 23, 2013 by robayedavies

Here are some slides:

– setting out a case for using DMDX with R to do reproducible science.

Posted in DMDX, rstats | Tagged , | Leave a comment

Getting started – drawing a scatterplot, with a linear regression smoother, edited title, label and theme, for report

Posted on April 22, 2013 by robayedavies

This post assumes that you have installed and are able to load the ggplot2 package, that you have been able to download the ML subject scores database and can read it in to have it available as a dataframe in the workspace, and that you have already tried out some plotting using ggplot2.

Here we are going to work on: 1. examining the relationship between pairs of variables using scatterplots 2. modifying the appearance of the scatterplots for presentation.

While doing these things – mostly achieving the presentation of relationships between variables – we should also consider what statistical insights the plots teach us.

1. Variation in the values of subject scores

We know that the participants tested in the ML study of reading varied on measures of gender, age, reading skill (we used the TOWRE test of ability, Torgesen, Wagner & Rashotte, 1999) and print exposure, a proxy for reading history (measured using the ART, Masterson & Hayes, 2007; Stanovich & West, 1989). What does the observation that participants varied mean?

In previous posts, we have seen how to use R to get a sense of the average for and spread of values on these measures for our sample, and we have seen how to show the distribution of values using histograms:

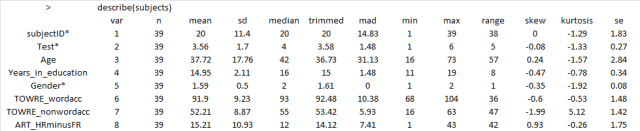
— using the function call: describe(subjects) to get the mean and standard deviation etc.

ML subjects descriptives 230413

— using the ggplot code discussed previously to get some histograms

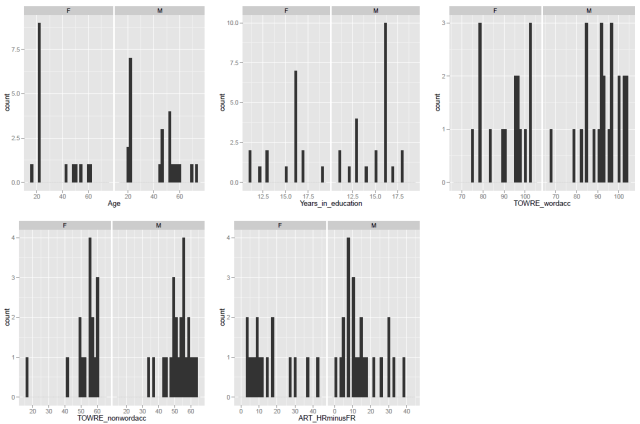
R-2-2-grid

What these numbers and these histograms show us is that participants in the sample varied broadly (from 20 years to 60+ years) in age, though most of the middle-aged people in the sample were male, also that measures of reading ability – TOWRE word and non-word naming accuracy – tended to vary around the top end of the range. Most people tested got at least three quarters of the items in each test correct, most of them did much better then that.

2. How do the variables relate to each other?

Let’s suppose that we are concerned about the relationship between two variables. How is variation in the values of one variable associated with change (or not) in the values of the other variable?

I might expect to see that the ability to read aloud words correctly actually increases as: 1. people get older – increased word naming accuracy with increased age; 2. people read more – increased word naming accuracy with increased reading history (ART score); 3. people show increased ability to read aloud made-up words (pseudowords) or nonwords – increased word naming accuracy with increased nonword naming accuracy.

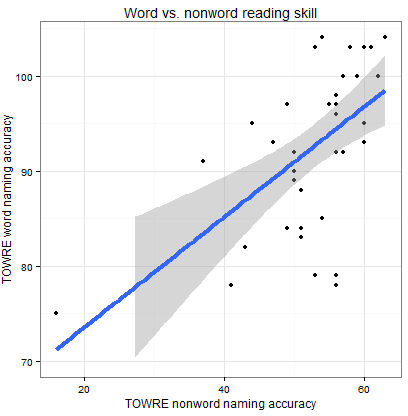
We can examine these relationships and, in this post, we will work on doing so through using scatter plots like that shown below.

R-3-1-subjects-scatter

What does the scatterplot tell us, and how can it be made?

Notice:

— if people are more accurate on nonword reading they are also often more accurate on word reading

— at least one person is very bad on nonword reading but OK on word reading

— most of the data we have for this group of ostensibly typically developing readers is up in the good nonword readers and good word readers zone.

I imposed a line of best fit indicating the relationship between nonword and word reading estimated using linear regression, the line in blue, as well as a shaded band to show uncertainty – confidence interval – over the relationship. You can see that the uncertainty increases as we go towards low accuracy scores on either measure. We will return to these key concepts, in other posts.

For now, we will stick to showing the relationships between all the variables in our sample, modifying plots over a series of steps as follows:

[In what follows, I will be using the ggplot2 documentation that can be found online, and working my way through some of the options discussed in Winston Chang’s book: R Graphics Cookbook which I just bought.]

Draw a scatterplot using default options

Let’s draw a scatterplot using geom_point(). Run the following line of code


ggplot(subjects, aes(x = Age, y = TOWRE_wordacc)) + geom_point()

and you should see this in R-studio Plots window:

R-3-1-scatter-default

Notice:

— There might be no relationship between age and reading ability: how does ability vary with age here?

— Maybe the few older people, in their 60s, pull the relationship towards the negative i.e. as people get older abilities decrease.

Distinguish groups by colour

Maybe I’m curious if gender has a role here. Is the potential age effect actually a gender effect? Get the scatterplot to show males and females observations in different colours using the following line of code:


ggplot(subjects, aes(x = Age, y = TOWRE_wordacc, colour = Gender)) + geom_point()

— All I did was to add …colour = Gender … to the specification of what data variables must be mapped to what aesthetic features: x position for a point is mapped to age; y position to reading ability; and now colour of point is mapped to gender, to give us:

R-3-1-scatter-colour

Notice:

— Males and females in the sample are now distinguished by colour.

— I do not see that the relationship between age and ability is modified systematically by the gender of the person.

— Maybe there is a different important variable: I would expect people who read more (and so have higher scores on the print exposure measure, the ART) to be better readers.

Distinguish variation in a continuous third variable by size

Group is a factor with two levels, male (coded as M in the dataframe) and female (F).

[See any introductory R or statistics book, e.g. Kabacoff’s “R in Action”, on which I draw to explain the following.]

Nominal variables are categorical (one thing or the other), e.g. gender. Ordinal variables are also categorical but imply order, e.g. agreement (disagree, agree, agree very much), though you cannot say that they imply amount because e.g. I cannot say if agree very much is twice the agree as disagree, patently that would be nonsense, but I can say that more agreement is there. Continuous variables can take any value between some range and imply order and amount. We can distinguish gender as a factor and word naming accuracy or age as continuous variables.

I am not sure how helpful it would be to vary colour of points by e.g. reading experience but we can do it:


ggplot(subjects, aes(x = Age, y = TOWRE_wordacc, colour =
ART_HRminusFR)) + geom_point()

— and while the plot looks nice, really, can you use the information added meaningfully?

R-3-1-scatter-colour-continuous

Notice:

— Higher ART scores are lighter and mostly appear in the older participants, not all of whom are among the better readers.

What about modifying point size in association with print exposure ART score?

Try this:


ggplot(subjects, aes(x = Age, y = TOWRE_wordacc, size =
ART_HRminusFR)) + geom_point()

R-3-1-scatter-size

Notice:

— It is clearer – hence, more useful – who’s scored higher on the print exposure measure.

N.B. I think there are data on how people perceive variation in colour vs. other dimensions and on the associated utility of varying such dimensions for data visualization (maybe work based on Cleveland’s experiments) and I will look them up some time.

— I get the feeling that print exposure is not going to help explain how reading ability varies for this sample.

Feelings are nice but let’s examine statistical relationships

I am going to start getting serious about this dataset. I want to look at all the relationships between word naming accuracy, reading ability, and all the other measures I have available, printing a grid of plots, as done previously. I am then going to impose an indication of the predicted relationship, given the data, between reading ability and the other variables.

First, the lattice of plots. We can combine our scatterplot code with the grid plotting code we used in an earlier post.


# produce a lattice of plots showing the relationship between word reading accuracy and the # other variables in this sample

# make plots

page <- ggplot(subjects, aes(x = Age, y = TOWRE_wordacc))
page <- page + geom_point()
page

pNW <- ggplot(subjects, aes(x = TOWRE_nonwordacc, y = TOWRE_wordacc))
pNW <- pNW + geom_point()
pNW

pART <- ggplot(subjects, aes(x = ART_HRminusFR, y = TOWRE_wordacc))
pART <- pART + geom_point()
pART

# print to pdf

pdf("ML-data-subjects-scatters-230413.pdf", width = 12, height = 4)

grid.newpage()

pushViewport(viewport(layout = grid.layout(1,3)))

vplayout <- function(x,y)
 viewport(layout.pos.row = x, layout.pos.col = y)

print(page, vp = vplayout(1,1))
print(pNW, vp = vplayout(1,2))
print(pART, vp = vplayout(1,3))

dev.off()

Notice:

— I am using # to comment on my code as I write it. R will ignore a line of text following the # (not a sentence, a line) e.g if you write: dothis() #  a function that does this, R will execute dothis() and ignore “a function that does this”.

That code produces a pdf of the lattice of plots:

R-3-1-scatter-grid

Notice:

— The age variable is really split between a bunch of 20s and a bunch of 40+s, the latter more widely spread than the former.

— I can see a relationship between word and nonword reading ability, which makes sense, but nothing else here.

Let’s see what relationship is indicated by a fitted regression model’s predictions for each pair of variables.

Modifying the code by : 1. adding the specification of a smoother using stat_smooth(), with 2. the addition of an argument to that function call asking for the smoother to be drawn using a linear model method.

Think of the smoother as a line showing the prediction of what the values on the y-axis variable – here, word naming ability – would be given the variation observed in the values of the x-axis variable – here, age, nonword naming ability, and print exposure. In these plots, each x-y relationship is considered separately, and we are assuming that the relationships are monotonic. We will get back to what these things mean later. Take a conceptual shortcut, we are asking: is reading ability predicted by age, nonword naming or reading history? We are examining: is that relationship of a kind where a unit increase in the x-axis variable is associated with a change in the values of the y-axis variable where the rate of the change is the same for all values of x?

For now, we focus on the plotting, and the code for adding lines indicating the relationship between word naming and age, nonword naming and print exposure is as follows:


# make plots

page <- ggplot(subjects, aes(x = Age, y = TOWRE_wordacc)) + geom_point() + stat_smooth(method=lm)

pNW <- ggplot(subjects, aes(x = TOWRE_nonwordacc, y = TOWRE_wordacc)) + geom_point() + stat_smooth(method=lm)

pART <- ggplot(subjects, aes(x = ART_HRminusFR, y = TOWRE_wordacc)) + geom_point() + stat_smooth(method=lm)

# print to pdf, opening device

pdf("ML-data-subjects-scatters-smoothers-230413.pdf", width = 12, height = 4)

# make grid

grid.newpage()

pushViewport(viewport(layout = grid.layout(1,3)))

vplayout <- function(x,y)
 viewport(layout.pos.row = x, layout.pos.col = y)

# print preprepared plots to grid

print(page, vp = vplayout(1,1))
print(pNW, vp = vplayout(1,2))
print(pART, vp = vplayout(1,3))

# turn device off

dev.off()

Which gets you this:

R-3-1-scatter-smoothers

Notice:

— As guessed earlier, increases in ART print exposure score are equally likely to be associated with an increase or a decrease in the word reading accuracy of participants – changes in print exposure do not predict or explain changes in reading ability.

— In contrast, people who score higher on the nonword reading test also score higher on the word reading test – variation in nonword naming ability do predict values in nonword naming ability.

— In between, I suspect that differences in age do not predict differences in word reading ability, if we were to take out the odd-looking older less able readers in the sample; but we will look at how we do that another time.

Statistics are nice but let’s polish the plots for presentation

You are starting to see the grey background of ggplot2 plots all over the media now, as more data-analysis-savvy organizations start to incorporate R into their work. However, let’s imagine that we wanted to report the plots in a paper and that we cannot ask people to print and copy plots with grey backgrounds. Imagine also that we wanted to change the titles and labelling of the plots to something more self-explanatory.

We can set the title of the graph using the ggtitle() function.

I want the range of the y-axis to be the same for all the plots – it will make them easier to compare – and I will use a scale function to do that.

I also think we could do with making the axis labels more meaningful, and I will use label functions to do that.

Lastly, we want to change the background to white from grey using the theme_bw() function.

First, I will illustrate these changes with one plot, in the following lines of code.


pNW <- ggplot(subjects,aes(x=TOWRE_nonwordacc, y=TOWRE_wordacc))
pNW <- pNW + geom_point() + ggtitle("Word vs. nonword reading
skill")
pNW <- pNW + xlab("TOWRE nonword naming accuracy") + ylab("TOWRE
word naming accuracy")
pNW <- pNW + ylim(70, 104)
pNW <- pNW + scale_x_continuous(breaks = c(20, 40, 60))
pNW <- pNW + theme(axis.title.x = element_text(size=25),
axis.text.x = element_text(size=20))
pNW <- pNW + theme(axis.title.y = element_text(size=25),
axis.text.y = element_text(size=20))
pNW <- pNW + geom_smooth(method="lm", size = 1.5)
pNW <- pNW + theme_bw()
pNW

Notice:

— I am adding each change, one at a time, making for more lines of code; but I could and will be more succinct.

— I first add the scatterplot points then the title with: + geom_point() + ggtitle(“Word vs. nonword reading skill”)

— I then change the axis labels with: + xlab(“TOWRE nonword naming accuracy”) + ylab(“TOWRE word naming accuracy”) 

— I fix the y-axis limits with: + ylim(70, 104)

— I change where the tick marks on the x-axis are with: + scale_x_continuous(breaks = c(20, 40, 60)) — there were too many before

— I modify the size of the axis labels for better readability with: + theme(axis.title.x = element_text(size=25), axis.text.x = element_text(size=20))

— I add a smoother i.e. a line showing a linear model prediction of y-axis values for the x-axis variable values with: + geom_smooth(method=”lm”, size = 1.5)  — and I ask for the size to be increased for better readability

— And then I ask for the plot to have a white background with: + theme_bw()

All that gets you this:

R-3-1-scatter-bw-smooth-edit

Next, we will redo the grid of plots, this time modified to improve readability, and also code concision, as follows.


# edited appearance - all plots in a word naming vs other variables grid of plots

# first create the plots

pNW <- ggplot(subjects,aes(x=TOWRE_nonwordacc, y=TOWRE_wordacc))
pNW <- pNW + geom_point() + ggtitle("Word vs. nonword reading
 skill")
pNW <- pNW + scale_y_continuous(name = "TOWRE word naming
 accuracy", limits = c(70, 104))
pNW <- pNW + scale_x_continuous(name = "TOWRE nonword naming
 accuracy", breaks = c(20, 40, 60))
pNW <- pNW + theme(axis.title.x = element_text(size=25),
 axis.text.x = element_text(size=20))
pNW <- pNW + theme(axis.title.y = element_text(size=25),
 axis.text.y = element_text(size=20))
pNW <- pNW + geom_smooth(method="lm", size = 1.5)
pNW <- pNW + theme_bw()


page <- ggplot(subjects,aes(x=Age, y=TOWRE_wordacc))
page <- page + geom_point() + ggtitle("Word reading vs. age")
page <- page + scale_y_continuous(name = "TOWRE word naming
 accuracy", limits = c(70, 104))
page <- page + scale_x_continuous(name = "Age (years)")
page <- page + theme(axis.title.x = element_text(size=25),
 axis.text.x = element_text(size=20))
page <- page + theme(axis.title.y = element_text(size=25),
 axis.text.y = element_text(size=20))
page <- page + geom_smooth(method="lm", size = 1.5)
page <- page + theme_bw()


pART <- ggplot(subjects,aes(x=ART_HRminusFR, y=TOWRE_wordacc))
pART <- pART + geom_point() + ggtitle("Word reading skill vs.
 print exposure")
pART <- pART + scale_y_continuous(name = "TOWRE word naming
 accuracy", limits = c(70, 104))
pART <- pART + scale_x_continuous(name = "ART score")
pART <- pART + theme(axis.title.x = element_text(size=25),
 axis.text.x = element_text(size=20))
pART <- pART + theme(axis.title.y = element_text(size=25),
 axis.text.y = element_text(size=20))
pART <- pART + geom_smooth(method="lm", size = 1.5)
pART <- pART + theme_bw()

# print to pdf

# open pdf device, naming file to be output

pdf("ML-data-subjects-scatters-smoothers-edited-230413.pdf", width = 12, height = 4)

# create grid

grid.newpage()

pushViewport(viewport(layout = grid.layout(1,3)))

vplayout <- function(x,y)
 viewport(layout.pos.row = x, layout.pos.col = y)

# orubt device to grid

print(page, vp = vplayout(1,1))
print(pNW, vp = vplayout(1,2))
print(pART, vp = vplayout(1,3))

# close device

dev.off()

All of which will get you this nice-looking and informative grid of plots:

R-3-1-scatter-grid-edit

Notice:

— There are many more things we could do in these plots, including:

1. Using different methods to generate the smoother, e.g. loess.

2. Add a line showing not the prediction of y-axis word naming on x-axis variable (age, nonword naming, ART) i.e. the bivariate relationship but the prediction of word naming on all variables considered together i.e. the multiple regression model predictions, using the function predict().

3. Add annotations to the plot e.g. variance explained by the model whose predictions we show, the R-squared.

4. Add vertical and horizontal lines that indicate the mean value for x-axis or y-axis variables.

5. Add marginal rugs to show the 1-D distribution of each variable.

6. Labelling specific points, sets of points, or all points.

What have we learnt?

The code used to generate the plots, and given as examples here, can be downloaded from here.

We have examined the distribution of single variables and learnt about variation in values.

We have then combined data from pairs of variables to examine, visually, the relationship between differences in the values of one variable and differences in the values of another.

We have seen how to edit the appearance of the plots to suit out needs.

key vocabulary

stat_smooth()

theme()

theme_bw()

stat_[x or y]_continuous()

ggtitle()

element()

References

Masterson, J., & Hayes, M. (2007). Development and data for UK versions of an author and title recognition test for adults. Journal of Research in Reading, 30, 212-219.

Stanovich, K. E., & West, R. F. (1989). Exposure to print and orthographic processing. Reading Research Quarterly, 24, 402-433.

Torgesen, J. K., Wagner, R. K., & Rashotte, C. A. (1999). TOWRE Test of word reading efficiency. Austin,TX: Pro-ed.

Posted in 7. Getting started - scatterplots, getting started, rstats | Tagged , , , , , , , , , | Leave a comment

Getting started – positioning and getting multiple plots on one page, output as a pdf

Posted on April 22, 2013 by robayedavies

This post assumes you know how to set a working directory, load a data file, and run a ggplot() function call to create a histogram using geom_histogram, as discussed here.

What are going to do in this post is expand our plotting vocabulary in order to achieve three things:

1. split the data by gender;

2. show histograms for all variables in ML’s database at the same time;

3. output the plots as a pdf for report.

In what follows, I assume the subjects database is in the workspace, and that the ggplot2 package library has been loaded.

1. Split the data by gender

In Exploratory Data Analysis, we often wish to split a larger dataset into smaller subsets, showing a grid or trellis of small multiples – the same kind of plot, one plot per subset – arranged systematically to allow the reader (maybe you) to discern any patterns, or stand-out features, in the data. Much of what follows is cribbed from the ggplot2 book (Wickham, 2009; pp.115 – ).

There is not too much going on in the subjects database, but we can start simply by splitting the data into gender subsets.

In ggplot2, faceting is a mechanism for automatically laying out multiple plots on a page.

Faceting generates small multiples each showing a different subset of the data. The facet function takes two arguments, the variables(-s) to facet by – which we deal with here – and whether position scales should be global or local to the facet – which we can deal with another time.

You can ask ggplot2 to facet plots in two different ways:

1. use facet_grid to split the data by two variables

2. use facet_wrap to split it by one.

We have only got gender to play with, so we’ll use facet_wrap.

Let’s build on the plot we did in the last post:


pAge <- ggplot(subjects, aes(x=Age))
pAge + geom_histogram() + facet_wrap(~Gender)

Notice:

— all we have done is add …facet_wrap(~Gender)

— this asks ggplot to generate a ribbon of small multiples split by gender, here, resulting in two plots, one for males and one for females in the sample:

R-2-2-facet

Notice:

— ML evidently tested many more females in their 20s and males in middle-age: psychology students are mostly female; the males are (I know) members of a club to which her father belonged.

2. Show histograms for all variables in ML’s database at the same time

The split by gender is nice. One day, we can use facetting more powerfully e.g. by showing data for every individual tested in a lexical decision task, to spot sample-wider patterns of individual differences in response.

For now, we will elaborate the plot a bit further, by plotting all variables in the subjects database on the same page, all split by gender. I will base what follows on ggplot book advice (pp. 151 – ). Wickham (2009) advises that arranging multiple plots on a single page involves using grid, an R graphics system, that underlies ggplot2.

We are going to create a faceted plot for each variable, and then assign them to places in a grid we shall also create. Copy-paste the following code in the script window to create the plots:


pAge <- ggplot(subjects, aes(x=Age))
pAge <- pAge + geom_histogram() + facet_wrap(~Gender)

pEd <- ggplot(subjects, aes(x=Years_in_education))
pEd <- pEd + geom_histogram() + facet_wrap(~Gender)

pw <- ggplot(subjects, aes(x=TOWRE_wordacc))
pw <- pw + geom_histogram() + facet_wrap(~Gender)

pnw <- ggplot(subjects, aes(x=TOWRE_nonwordacc))
pnw <- pnw + geom_histogram() + facet_wrap(~Gender)

pART <- ggplot(subjects, aes(x=ART_HRminusFR))
pART <- pART + geom_histogram() + facet_wrap(~Gender)

Notice:

— I have given each plot a different name. This will matter when we assign plots to places in a grid.

— I have changed the syntax a little bit: create a plot then add the layers to the plot; not doing this, ie sticking with the syntax as in the preceding examples, results in an error when we get to print the plots out to the grid; try it out – and wait for

>Error: No layers in plot

You will see the plot window in R-studio fill with plots as the code gets executed, each following plot replacing the earlier one in the script. You will also see the plots get listed as objects in the Workspace window.

What we will do is make a grid for the plots, using the grid.layout() function to set up a grid of viewports. We will specify how many rows and columns of plots we want. We draw each plot into its own position on the grid. We create a function to save typing, and then draw each plot in its place on the grid. [I am copying this almost verbatim from the ggplot book, indicating my limited understanding of the mechanics at work, here.]

We have five plots we want to arrange, so let’s ask for a grid of 2 x 3 plots ie two rows of three.


grid.newpage()

pushViewport(viewport(layout = grid.layout(2,3)))

vplayout <- function(x,y)
viewport(layout.pos.row = x, layout.pos.col = y)

Notice:

— Today, for the first time, running grid.newpage() resulted in the error:

Error: could not find function “grid.newpage”

— which can be fixed by running:  library(grid)  

— this is noteworthy because I would have thought that the grid() package would get loaded together with ggplot2(), anyway… I’ll keep my eye out for that one.

Having asked for the grid, we then print the plots out to the desired places, as follows:


print(pAge, vp = vplayout(1,1))
print(pEd, vp = vplayout(1,2))
print(pw, vp = vplayout(1,3))
print(pnw, vp = vplayout(2,1))
print(pART, vp = vplayout(2,2))

As R works through the print() function calls, you will see the Plots window in R-studio fill with plots getting added to the grid you specified.

3. Output the plots as a pdf for report

Let’s say we have constructed a wonderful plot. We now want to use it elsewhere, as a figure in a report or on a slide in a talk, or as an image in a web post. Naturally, this being R, you start by thinking about what you want, as you can have pretty much whatever that might be.

You can ask for two kinds of output, vector graphics (infinitely zoomable) or raster graphics (stored as an array of pixels, with one good viewing size). After a bad experience with figures for a paper, I now tend to output vector graphics i.e. pdfs – which integrate nicely in latex/beamer slides and can be pasted into word documents from a screen shot (I know, I’m sure there’s a better way). You can also use the ggsave() function but I never learnt that though I’m open to advice.

Wickham (2009; p. 151) recommends differing graphic formats for different tasks, e.g. png (72 dpi for the web); dpi = dots per inch i.e. resolution.

Most of the time, I output pdfs. You call the pdf() function – a disk-based graphics device -specifying the name of the file to be output, the width and height of the output in inches (don’t know why, but OK), print the plots, and close the device with dev.off(). You can use this code to do that.


pdf("ML-data-subjects-histograms-220413.pdf", width = 15, height = 10)

print(pAge, vp = vplayout(1,1))
print(pEd, vp = vplayout(1,2))
print(pw, vp = vplayout(1,3))
print(pnw, vp = vplayout(2,1))
print(pART, vp = vplayout(2,2))

dev.off()

Which results in a plot that looks like this:

R-2-2-grid

Notice:

— It looks like males and females in the sample are fairly matched on reading ability but differ on age, education and reading experience (ART).

— If it were a jpeg, you’d specify width and height in pixels (don’t ask me why, there is a reason but I forgot it).

What height-width ratio to use? I don’t know, try the golden ratio. Sometimes I remember to think about it but usually I just look, and adjust the code as required. Try it. Obviously, do not have the pdf of the plot open when running the code (try that and see what happens).

What have we learnt?

You can download the code to draw the plots in this post here. Obviously, you’ll need to go back a post to see how to load the the data which you can get here.

We have learnt how to create small multiples of plots in ggplot2 using facetting. This will come in much handier as our data gets more complicated. We have also learnt how to use grid() to plot multiple variables at once. And we have learnt how to output our plots as a pdf for later use.

Key vocabulary

graphics device

ggplot()

geom_histogram()

facet_wrap()

pdf()

grid()

print()

Posted in 6. Getting started - grid plots, plotting data, rstats | Tagged , , , , , , , , | 1 Comment